New Encoding/Decoding Methods for Designing Fault-Tolerant Matrix Operations

D.L. Tao, C.R.P. Hartmann, and Yunghsing S.(Sam) Han

IEEE TRANSACTIONS ON PARALLEL AND DISTRIBUTED SYSTEMS, VOL. 7, NO. 9, SEPTEMBER 1996, pp. 931-937

Abstract

Algorithm-based fault tolerance(ABFT) can provide a low-cost error protection for array processors and multiprocessor systems. Several techniques have been proposed to design fault-tolerant matrix operations. In this paper, new encoding/decoding methods are proposed for designing fault-tolerant matrix operations. The unique feature of these new methods is that only additions and subtractions are used in encoding/decoding.

  1. Introduction

The advantage of ABFT is that errors which are caused by permanent or transient failures in the system can be detected/corrected by using a very low overhead and at the original throughput.

During system normal operation, the probability of having more than two faults is negligible. Two new encoding/decoding algorithms to construct error detecting/correcting codes with the minimum Hamming distance 3 and 4 are respectively proposed in this paper.

  1. A Brief Review

In this section, we evaluate existing ABFT techniques which are used to perform fault tolerant matrix-vector multiplications. The following check matrix, H with dimension , is used to construct a code with the minimum distance :

  1. Single Error Correction

For single error correction, i.e., the minimum Hamming distance is 3, the check matrix given has the following form:

1) Jou-Abraham’s scheme

let ,

2) Luk and Park’s scheme

let ,

3) A similar is proposed in [10].

,where

  1. Single Error Correction/Double Error Detection

Minimum Hamming distance 4 code is needed.

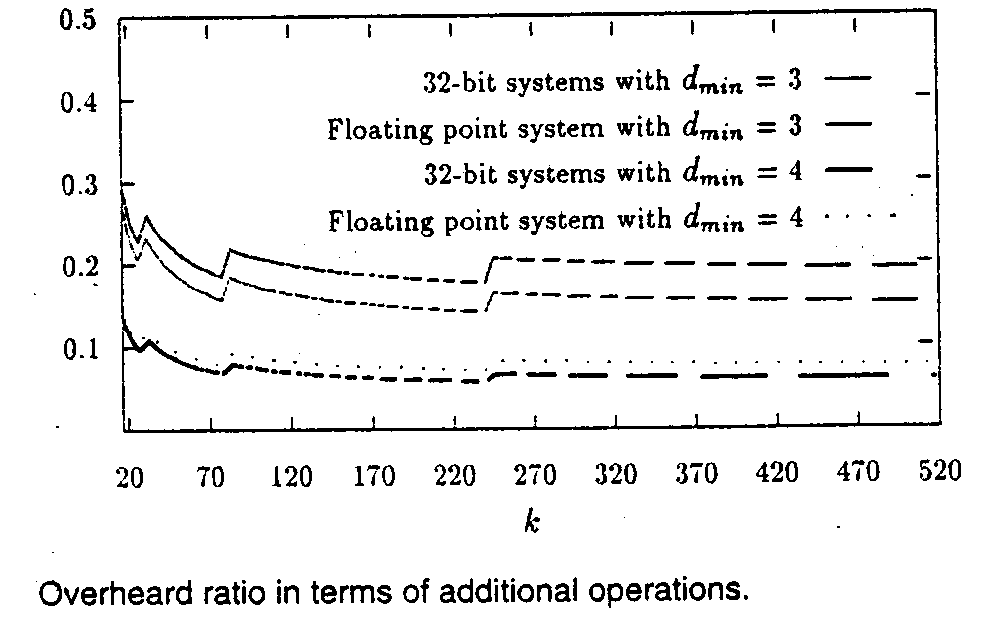
The overhead of encoding/decoding as given in the previous subsection is shown in Table 1.

  1. Partial Check-Sum: New Encoding/Decoding Schemes

The encoding/decoding methods proposed in this paper can be described by a check matrix . The new methods use only addition/subtractions so that the overhead will reduced significantly.

 

  1. Lengthened Hamming Codes (LHC)

In this subsection, we introduce the Lengthened Hamming Codes (LHC) with the minimum Hamming distance 3. So it can correct all single errors. The Lengthened Hamming Codes (LHC) can be constructed by the check matrix .

 

Procedure I.

Step1: Let denote the number of information (check) digits. For a given k, find the minimum r to satisfy:

Step2: For the r found in Step1, find the minimum r’, where r’, to satisfy:

Step3: Let be the set containing all r-digit vectors which contain 1s, -1s, and (r--) 0s, where +’and .

Step4: Let be the set containing all r-digit vectors which contain 1s, -1s, and (r-2*) 0s, where 2*’. Partition into and such that

    1. =∪,

    2. for every element , we can find an element such
that s+t=0.

Step5: =∪.

Step6: Let denote the cardinality of S. If -k > 0, then delete -k elements from S arbitrarity.

 

Step7: is an r * ( k+r ) dimensional matrix. In the transpose of , , each element in S is used as a row vector in the first k rows, the last r rows of is the negative identity matrix.

 

Example1.

Let us construct an -matrix for k=26 by using Procedure I. Since k=26, r=4, r’=3. The element in are listed in the following table.

 

j

j

Elements in S

2

2

3

2

2

2

0

0

0

1

1

1

1100,1010,1001,

0110,0101,0011,

0111,1011,1101,1110

011-1,101-1,110-1,11-10,

01-11,10-11,1-101,1-110,

0-111,-1011,-11-1,-1110.

 

The element in are listed in the following table.

 

Elements in S

Elements in S

-1100,-1010,-1001

0-110,0-101,00-11

1-100,10-10,100-1

01-10,010-1,001-1

 

An is constructed as follows:

=

 

 

By using LHC, r additional check digits will be used. The relationship between k and r and the ratio between k and r in LHC are shown in Table2.

Table 2

The Relationship Between k and r in LHC

k

5 ~10

11~36

37~116

117~358

r

3

4

5

6

0.6~0.30

0.36~0.11

0.14~0.04

0.05~0.02

 

  1. A Single Error Correction/Double Error Detection(SEC/DED) Code

In this subsection, we construct the a code with the minimum Hamming distance 4, which can correct all single errors and detect all double errors. The SEC/DED can be constructed by the check matrix .

 

Procedure II.

Step1: for a given k, find the smallest r to satisfy the following inequality:

.

Step2: Let S be the set containing all r-digit vectors which have odd weight except three, provide that each vector contains exactly one -1.

Step3: Let denote the cardinality of S. If -k > 0, then delete -k elements from S arbitrarily.

Step4: is an r * ( k+r ) dimensional matrix. In the transpose of , , each element in S is used as a row vector in the first k rows, the last r rows of is the negative identity matrix.

 

 

Example2.

Let us construct an -matrix for k=15 by using Procedure II. Since k=15, r=6. An is shown as follows:

=

 

The relationship between k and r and the ratio between k and r in this new code are shown in Table3.

Table 3

The Relationship Between k and r in the SEC/DED Code

k

6~30

31~112

113~436

437~787

r

6

7

8

9

1~0.20

0.26~0.06

0.07~0.02

0.02~0.01

 

  1. Fault-Tolerant Matrix Operations

where , .

  2. Overhead Evaluation

  1. Single Error Correction

Table 4

Overhead Comparisons when =3(single error correction) where r satisfies step1 of procedure I

   

encoding

matrix-vector multiplication

decoding

total

weighted check-sum

multiplications

k

2k

k

k+3k

additions

2k(k-1)

2(k-1)

2(k-1)

2 k+2k

LHC

multiplications

0

r*k

0

r*k

additions

c*r*k

r(k-1)

c*r*k

r(c k+ck+k-1)

 

, where l is the word length.

  1. Single Error Correction/Double Error Detection

Table 5

Overhead Comparisons when =4(SEC/DED) where r satisfies step1 of procedure II

   

encoding

matrix-vector multiplication

decoding

total

weighted check-sum

multiplications

2k

3k

2k

2k+5k

additions

3k(k-1)

3(k-1)

3(k-1)

3 k+3k

SEC/DED

multiplications

0

r*k

0

r*k

additions

r*k

r(k-1)

r*k

r( k+3k+1)

 

, where l is the word length.

  1. Concluding

 

 

Created by : Chuang Yuh-Jue

Date : June 3, 1997