An Algorithm for the Banded Symmetric Generalized Matrix Eigenvalue Problem

Linda Kaufman

Siam J. Matrix Anal. Appl., Vol. 14, No. 2, pp.372-389, Apri. 1993

 

1. Introduction

In this paper we consider the generalized eigenvalue problem :

where and are both symmetric and positive definite matrices and both are banded with nonzero diagonals. And we can find that if is nonsingular then

so

  1. The Martin and Wilkinson method

step1. Cholesky factorization of

then forming

reducing to tridiagonal form , this step requires time.

 

step2. Finding the eigenvalues of the tridiagonal matrix , this step require time.

  1. The QZ algorithm of Moler and Stewart

This algorithm require time.

  1. The algorithm of Wang and Zhao

The algorithm is based on the theorem of Stewart about the singular value decomposition (SVD) of portions of orthogonal matrix. Consider the Cholesky factorization of and

(2.1)

(2.2)

and the QR decomposition

(2.3)

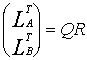
where is a matrix with orthonormal columns, is upper triangular, and nonsingular.

Partition into

(2.4)

from (2.3) and (2.4) we get

(2.5)

and

(2.6)

If and x satisfy the general eigenvalue problem then from (2.1) and (2.2)

and from (2.5), (2.6) implies

(2.7)

the SVD of and is

(2.8)

(2.9)

where , , and are all orthogonal matrices, and are diagonal matrices , .

Then because of the orthogonality of the columns of in (2.3)

and

(2.10)

we let from (2.7), (2.8) and (2.9)

(2.11)

letting and multiplying both side of (2.11) by

so

(2.12)

from (2.10)

(2.13)

Algorithm W.Z

(1)

(2) Let find orthogonal transformation such that

(3)Determine let

(4)Reduce to bidiagonal form

(5)find the SVD of to obtain singular values then the eigenvalues given by (2.13) .

step (1) -(4) needs time.

step (5) need time.
  1. Modifying the Wang-Zhao to tridiagonal matrices

3.1 Decreasing the fill-in in in step(2) of the W.Z algorithm

the in W.Z algorithm is

where “+” indicates a new nonzero element the in W.Z

The modified algorithm

let to get , is designed to annihilate and is to annihilate the remaining elements in the ith column below the diagonal.

so step (2) require .

 

3.2 Decreasing the fill-in in .

The same we can decrease step (3) from to to get the tridiagonal matrix

Created by: Wen-Yan Tian

Date: Apr 17 1997