首先分析矩陣的運算在
Convex的機器上跑有沒有加速我的原始式碼是
1. #include <stdio.h>
2. #include <stdlib.h>
3. #include <time.h>
4. #define N 500
5. void initmatrix(int n);
6. void multmatrix(int n);
7. int a[N][N],b[N][N],c[N][N],d[N][N];
8. int i,j,k,n;
9.
10.main()
11.{
12. time_t s_t, e_t;
13. double dif_time;
14. for(n=100;n<=N;n=n+100){
15. time(&s_t);
16. initmatrix(n);
17. multmatrix(n);
18. time(&e_t);
19. dif_time = difftime(e_t, s_t);
20. printf("n = %d time unit = %f\n",n,dif_time);
21. }
22. }
23.
24.void initmatrix(int n)
25.{
26. for(i=0;i<n;i++){
27. for(j=0;j<n;j++){
28. a[i][j]= (rand()%100);
29. b[i][j]= (rand()%100);
30. c[i][j]= 0;
31. }
32. }
34.}
35.void multmatrix(int n)
36.{
37. for(i=0;i<n;i++){
38. for(j=0;j<n;j++){
39. for(k=0;k<n;k++){
40. c[i][j]= c[i][j] + a[i][k]*b[k][j];
41. }
42. }
43. }
44.}
用
% cc -O3 -or loop -tm c2 matrix.c的指令去編譯產生最佳化的程式碼並可列出對loop平行化或向量化的資料,資料如下Optimization for Procedure main
Line Id Iter. Reordering New Optimizing / Special
Num. Num. Var. Transformation Loops Transformation
-----------------------------------------------------------------------------
14 1 *NONE* Scalar
Line Id Iter. Analysis
Num. Num. Var.
-----------------------------------------------------------------------------
14 1 *NONE* No induction variable
Optimization for Procedure initmatrix
Line Id Iter. Reordering New Optimizing / Special
Num. Num. Var. Transformation Loops Transformation
-----------------------------------------------------------------------------
26 1 *NONE* Scalar
27 2 *NONE* Scalar
Line Id Iter. Analysis
Num. Num. Var.
-----------------------------------------------------------------------------
26 1 *NONE* No induction variable
27 2 *NONE* No induction variable
Optimization for Procedure multmatrix
Line Id Iter. Reordering New Optimizing / Special
Num. Num. Var. Transformation Loops Transformation
-----------------------------------------------------------------------------
36 1 i *Dist (2-4) No Strip
36-1 2 i PARA/VECTOR
36-2 3 i PARALLEL
37-2 5 j FULL VECTOR
36-3 4 i PARALLEL
37-3 6 j FULL VECTOR Inter
38-3 7 k Scalar
Line Id Iter. Analysis
Num. Num. Var.
-----------------------------------------------------------------------------
36-1 2 i Parallel outer strip mine loop
37-3 6 j Interchanged to innermost
從分析中看出
Convex在陣列指定起初值時,沒有什麼平行化的表現出現,但是在陣列的相加,相乘等運算中則有明顯的向量,平行化的運算利用上,以下是所得出的結果n
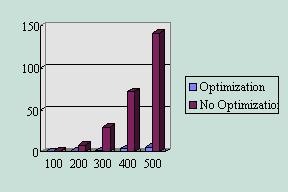
是矩陣的大小n*n time unit 是執行的時間 單位是秒==================================================
n = 100 time unit = 0.000000
n = 200 time unit = 1.000000
n = 300 time unit = 2.000000
n = 400 time unit = 4.000000
n = 500 time unit = 6.000000
在
convex上用指令cc -no matrix.c來把平行化的作用禁能所跑出來的結果是n = 100 time unit = 1.000000
n = 200 time unit = 8.000000
n = 300 time unit = 29.000000
n = 400 time unit = 72.000000
n = 500 time unit = 141.000000

由圖表可知
Convex在矩陣運算中可得到很好的效果
在排序方面
Convex的表現,我所用的程式是1. #include <stdio.h>
2. #include <stdlib.h>
3. #include <time.h>
4. #define MAX 500000
5. void quick_sort(int *a,int left,int right);
6. int Data[MAX];
7. main()
8. {
9. time_t s_t,e_t;
10. double dif_time;
11. int i,n;
12. for(n=100000;n<=MAX;n=n+100000){
13. time(&s_t);
14. for(i=0;i<n;i++){
15. Data[i]=rand()%100;
16. }
17. quick_sort(Data,0,n-1);
18. time(&e_t);
19. dif_time= difftime(e_t,s_t);
20. printf("Data size = %d excute time = %f\n",n,dif_time);
21. }
22.}
23.void quick_sort(int *a,int left,int right)
24.{
25. int i, j, key, temp;
26. if(right > left)
27. {
28. key = a[right];
29. i = left - 1;
30. j = right;
31. while(1)
32. {
33. while(a[++i] < key);
34. while(a[--j] > key);
35. if(i >= j) break;
36. temp = a[i];
37. a[i] = a[j];
38. a[j] = temp;
39. }
40. temp = a[i];
41. a[i] = a[right];
42. a[right] = temp;
43. quick_sort(a, left, i-1);
44. quick_sort(a, i+1, right);
45. }
用最佳化的指令編譯
Optimization for Procedure main
Line Id Iter. Reordering New Optimizing / Special
Num. Num. Var. Transformation Loops Transformation
-----------------------------------------------------------------------------
12 1 n Scalar
14 2 i Scalar
Line Id Iter. Analysis
Num. Num. Var.
-----------------------------------------------------------------------------
12 1 n Inner loop has varying trip count
14 2 i Insufficient vector code
Optimization for Procedure quick_sort
Line Id Iter. Reordering New Optimizing / Special
Num. Num. Var. Transformation Loops Transformation
-----------------------------------------------------------------------------
31 1 *NONE* Scalar
33 2 *NONE* Scalar
34 3 *NONE* Scalar
Line Id Iter. Analysis
Num. Num. Var.
-----------------------------------------------------------------------------
31 1 *NONE* No induction variable
33 2 *NONE* No induction variable
34 3 *NONE* No induction variable
演算法中
loop部份大都未被平行或向量化,因為排序演算是對陣列中的鍵值做運算,並不像矩陣的運算有大量陣列的運算所以不容易平行或向量化,跑出來的結果如下Data size = 100000 excute time = 1.000000
Data size = 200000 excute time = 2.000000
Data size = 300000 excute time = 3.000000
Data size = 400000 excute time = 5.000000
Data size = 500000 excute time = 5.000000
而未對程式做任何最佳化處理的指令
cc -no quicksort.c所跑出來的結果是Data size = 100000 excute time = 2.000000
Data size = 200000 excute time = 3.000000
Data size = 300000 excute time = 4.000000
Data size = 400000 excute time = 6.000000
Data size = 500000 excute time = 8.000000
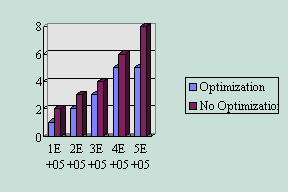
由圖可知排序演算在
Convex上的最佳化的幅度不會很大,是因為沒運用上向量或平行化的特性,最佳化的程式有比原來的效率好一點的原因,可能是編譯時有稍微程式碼最佳化的特性出現。