Parall Algorithm
期末程式報告
主題
CONVEX C3840
上程式平行化學生
: 陳建明 學號:8524611概論
一般的程式在一般的單
CPU架構上執行。 如果我們用更多的CPU, 或是其它較特別的架構下, 應該會有較單CPU的電腦有更好的執行效率。 而這次做的程式平行化是在C3840上所做Matrix相乘程式的平行化。這次所用的硬體是
CONVEX C3840擁有四個中央處理機共 512 MB 的主記憶體, 其中Communication Registers有32組的全域暫存器, 每一組有128單位。CONVEX C3840是pipelined vector Computer, 應用pipeline的技術讓連續相同的運算減少運算時間。所以在C3840上加速必需要讓資料向量化, 相同的運算集中, 才能有C3840應該有的效率。一般的程式在
C3840上要平行化, 只要會一般program的技術和向量技術的概念, 再利用中山C3840上的平行最佳化的compiler, 將程式編譯成向量化程式。C語言編輯程式有五個基本最佳化的選擇, 這五個基本選項分別是:
-no :
不做任何最佳化。-O0:
作Local的純量(Scalar)計算最佳化。-O1:
作Global的純量(Scalar)計算最佳化。-O2:
作向量(Vector)計算最佳化。-O3:
作平行計算處理最佳化。
O0,O1
的最佳化:
X=Y+C; X=X*4; T=X*B+1; X=1; |
Optimized Code:
REG=Y+C; REG=REG+4; T=REG*B+1; X=1;
|
REG: registers;
O2
的最佳化:
DO I=1,N DO J=1,N DO K=1,N A(I,J,K)=B(I,J,K) ENDDO ENDDO ENDDO |
Compiled Code:
DO K=1,N DO J=1,N DO I=1,N A(I,J,K)=B(I,J,K) ENDDO ENDDO ENDDO |
O3
的最佳化:
DO J=1,200 DO I=1,200 A(I,J)=B(I,J) ENDDO ENDDO |
Compiled Code: divide into 4 CPUs DO J=1,50 DO I=1,200 A(I,J)=B(I,J) ENDDO ENDDO
DO J=51,100 DO I=1,200 : DO J=101,150 DO I=1,200 : DO J=151,200 DO I=1,200 : |
在程式方面由於記憶體是
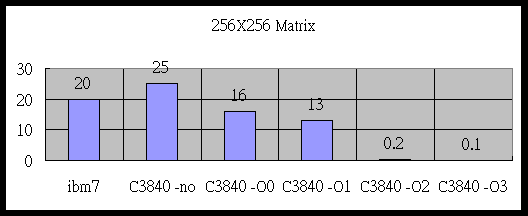
Column major所以在程式分為兩個部分來測試,一部分是不改變array和matrix的相對位置,而弟二個部分是將第二個matrix在array上做row和column交換。256x256 matrix MA MB
相乘所需的時間(單位second) 。|
ibm7 |
C3840 -no |
C3840 -O0 |
C3840 -O1 |
C3840 -O2 |
C3840 -O3 |
|
20 |
25 |
16 |
13 |
0.2 |
0.1 |

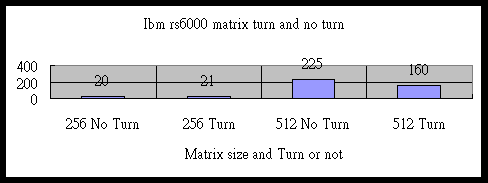
Ibm7 Matrix turn column to row
|
256 No Turn |
256 Turn |
512 No Turn |
512 Turn |
|
20 |
21 |
225 |
160 |
512X512 Matrix MaxMB
所需的時間(單位second)|
ibm7 |
C3840 -no |
C3840 -O0 |
C3840 -O1 |
C3840 -O2 |
C3840 -O3 |
|
225 |
202 |
134 |
94 |
1.4 |
0.4 |
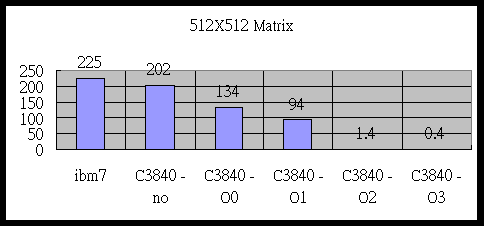
由第一
,第三個圖表, 可以發現平行化的level愈高,所需的時間就愈少。而且我們可以發現,沒有最佳化和最佳化,所需要的時間相差上佰倍,所以vector computer有其功用。因為沒有最佳化的程式和一般ibm rs6000工作站時間相差不多。所以使用了C3840要用最佳化的選項來編譯程式。由第二個圖表可以發現
,在matrix size是256x256時,因為column turn to row 花了一些時間, 所以比沒有turn 所需的時要多。但是在 512X512 時,有turn的時間明顯的比沒有轉換的要多。因為在size 較大的時候memory的address相差較大,所以要從新load資料的機率就增大了。但是在另一方面,在做了O2,O3的最佳化後,反而所有的row to column的轉換變成了多餘的,多花了不少的時間。