Parallel Algorithm
Final Report
The sorting and matrix multiplication in PVM environment
授課老師 : 楊昌彪
Institute of Computer and Information Engineering
Name :
盧天麒(Tain-chi Lu)Student ID : 8534804
Date : 1997/6/30
1. Introduction
PVM (Parallel Virtual Machine) is a software package that permits a heterogeneous collection of Unix computers hooked together by a network to be used as a single large parallel computer. Thus large computational problems can be solved more cost effectively by using the aggregate power and memory of many computers. The software is very portable.
PVM enables users to exploit their existing computer hardware to solve much larger problems at minimal additional cost. Hundreds of sites around the world are using PVM to solve important scientific, industrial, and medical problems in addition to PVM's use as an educational tool to teach parallel programming. With tens of thousands of users, PVM has become the defacto standard for distributed computing world-wide. The overall objective of the PVM system is to enable such a collection of computers to be used cooperatively for concurrent or parallel computation.

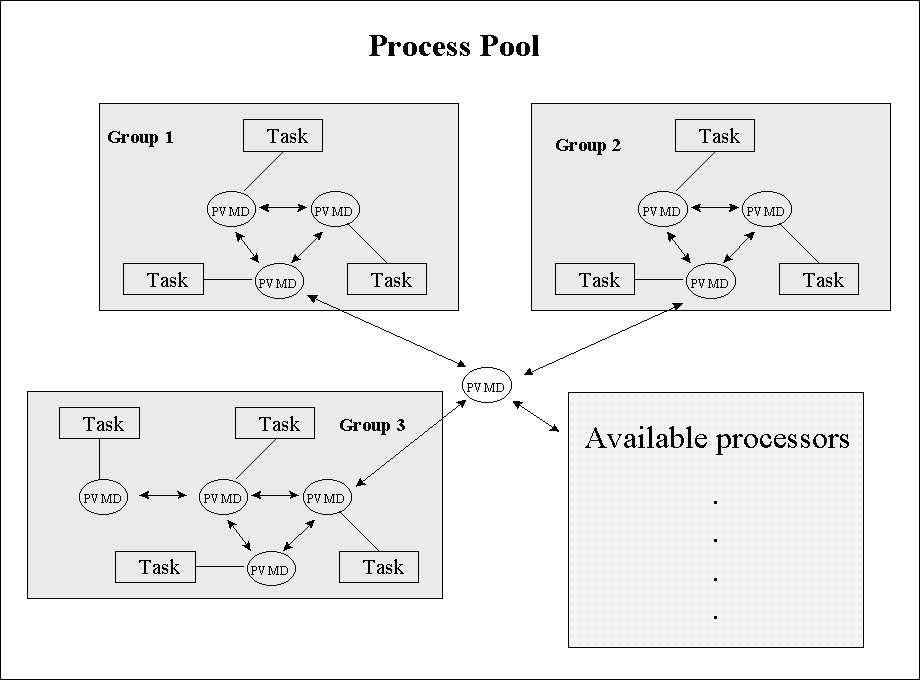
Figure 1. Process Pool in PVM’s environment
2. Experimental Protocol
The performance evaluation of network computing and its applications for some parameters and algorithms have been scatterly reported in the literature. Cap and Strumpen presented the method of heterogeneous partitioning and compared it with the method of homogeneous partitioning. They also evaluated the performance of several platforms, such as the Parform, PVM, Linda, POSYBL, and Transputer MC-2/32-2. They reported that the dynamic load balancing is an essential technique to achieve high performance. Strumpen and Casavant considered the contention for LAN-based networks and latency for WAN-based networks.
The contribution of performance characterization on network computing and its applications are scatterly seen in the literature. Perhaps it is worthwhile to put them all in one place so that another network computing researcher can save from collecting the methods and redoing the tedious experiments himself or herself. The main performance factor to be measured is speedup. The speedup is defined as the sequential execution time divided by the parallel execution time. The speedup currently is measured in the wall-clock time.
2.1 Hardware/Software Environment
Network configuration
Network computing may consist of homogeneous or heterogeneous environment. For homogeneous environment where each computing node is of the same machine type, the measurement of some performance such as speedup tells what speed can be gained or saturated, if more workstations are added to the computing environment. However, for the heterogeneous environment where the computing power of each machine might vary significantly, it is hard to tell what workstation contributes how much computation to the speedup. In order to get a uniform measurement of performance for speedup comparison, the computing power of each machine type should be measured first. To avoid the fluctuation in the measurements of computing power, the fifty measurements are taken for each type of workstations over several time slots. The mean of the measurements is used. Currently the heterogeneous environment consists of HP 715/33, Sun Sparc 2, and Sparc 20 workstations. The same type of workstations have the same hardware configuration including the size of RAM, cache memory, and hard disk. Of course, the ideal test platform is an isolated controllable environment where one can demonstrate how the parameters affect the performance, without interference from outside world. However, in the real world, it is impractical to create such environments. Instead of using an isolated controlled environment, we run the experiments over a variety of time slots and use statistical analysis to remove the outliers.
Bandwidth and Startup Time
The evolution of network technologies has made feasible high performance computing of local area network, metropolitan area network, and wide area network connected workstations cluster. Different networks, such as Ethernet, FDDI and ATM, have different communication bandwidth, and thus will affect the overall performance. For example, the limiting factor for LAN-based network is contention, but for WAN network is latency. The parameters related to communication speed should be extracted first in order to estimate analytically the communication overhead of various applications implemented on workstation clusters.
The communication time of sending one byte of data through a network can be expressed as
![]()
where ![]() is the startup time to send a batch of data; mtu is the maximum transfer unit of the specific network;
is the startup time to send a batch of data; mtu is the maximum transfer unit of the specific network; ![]() is the packet time to pack up the data of length mtu;
is the packet time to pack up the data of length mtu; ![]() is the communication time of sending one byte of data; l is the total length of data (in units of bytes) to be sent. Sometimes for simplicity, the effect of
is the communication time of sending one byte of data; l is the total length of data (in units of bytes) to be sent. Sometimes for simplicity, the effect of ![]() and
and ![]() is merged into another single parameter
is merged into another single parameter ![]() and the above equation is changed into
and the above equation is changed into
![]()
In order to acquire these communication parameters, we conduct a test on our communication network where one machine sends out data of various length to another machine which sends back an acknowledgment upon receiving the data. The measurement is done for pairs of different types of workstations (in heterogeneous environment) as well as workstations in different LAN subnets (workstations clusters spanned over more than on subnet). We also measure the parameters for a task to send data to another task in the same machine in which case the communication time is usually ignored. Figures 2 show the measurement results according to the Table 1.
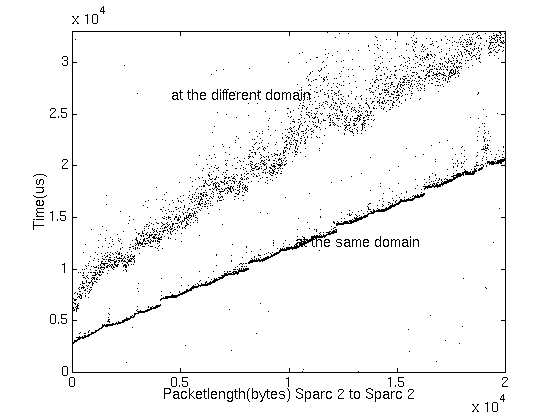
Figure 2. Communication time vs. data length for SPARC2-to-SPARC2 communication on Ethernet. The lower group of data is from two SPARC2 machines on the same subnet while the upper group of data is from two SPARC2 machines on different subnet.
Table 1. The measured data for the communication parameters under different configuration. Some parameters (marked by *) for machines in different subnet are hard to characterize due to the randomness of the measured data.
(ms) |
(ms) |
mtu (bytes) |
(us/byte) |
(us/byte) |
|
sparc2-sparc2 (same subnet) |
3 |
1.0 |
4096 |
0.854 |
1.125 |
sparc2-sparc2 (diff. subnet) |
6 |
* |
* |
* |
0.9 |
sparc2 (same machine) |
3 |
1.0 |
4096 |
0.25 |
0.5 |
sparc10-sparc10 |
3 |
1.125 |
|||
sparc20-sparc20 |
2 |
1024 |
1.125 |
Number of Workstations
The speedup usually increases in accordance with the number of workstations. It is an important parameter to show how much speedup can be improved by adding processors. But the speedup is not necessarily increasing without limitation by adding more processors. In heterogeneous environment, the workstation number is replaced by the normalized computing node number by measuring the relative computing power of each composing node.
Parallel Computing Platform
A number of programming environments exist that make distributed computing available to the application programmer. Among them are PVM, P4, Parform, Express, …etc. Here, the public domain PVM is used as the parallel computing platform throughout the paper.
2.2 The Parameters of Applications
Problem Domain
The performance of network computing is mainly dependent on the applications. Some of applications need to communicate a large volume of data; others may need a faster computation power. For different requirements the design of algorithms will be different. Hence it is required to state the characteristics of the applications.
Problem Size
The system performance for a particular application will change for different problem size. The ideal case for the speedup versus the problem size is expected to be a linear relationship. Due to communication overhead and others factors, the relation may not be linear at both ends of the curve.
Data Type
While an unsophisticated parallel scheme gives good performance on a scene with even distribution, it may give a poor performance when load distribution is highly non-uniform. For example, in the matrix computations, the execution time for dense matrices and sparse matrices has significant difference even for the same matrix size. In graphic render problem, the performance of algorithms may have different behavior under different image data type, and thus it needs to be taken into consideration.
Algorithm Selection
There may exist several algorithms for each application problem. Some algorithms are inherently sequential and not parallelizable. Others might perform poorly when executed in a single machine, but have excellent performance when run under parallel environment. Furthermore, some algorithms may have efficient speedup in dedicated multiprocessor system, such as Intel Hypercube, but cannot have the same performance on workstation clusters. There are several issues to consider during the implementation of the algorithms:
The algorithm performs a distributed matrix multiplication on a mesh of processors. Let the two input matrices be A and B, and the product C. Consider a 4 * 4 mesh of processors. The domain decomposition of B and C is straightforward. Each processor is given a submatrix of the same size. (The matrix may have to be padded with zeros to accomplish this.)
The three stages of the algorithm, (broadcast, multiply, roll) are repeated once for every row in the processor mesh.
In each row of processors, one processor copies the A matrix into a matrix, T. Then this T matrix is broadcast to the rest of the processors in the row. The broadcast is done left to right (with the rightmost processor passing to the leftmost processor). In the first broadcast in our example of a 4 * 4 mesh the diagonal processes would copy the A matrix in the T matrix.
Next the diagonal processes pass the T matrix to the right. This continues until the matrix has been broadcast to the entire row.
In each processor, the product of T and B submatrices is added to the C submatrix.
In each processor, the B submatrix is passed to the processor to the north.
The C submatrices can be written as sums of products of the A and B submatrices.
A more subtle way to avoid concurrent-read operations from the same memory location in procedure CREW SORT is to remove the need for them.
4. Experimental Results
The workstations used for the experiments includes twelve HP 715/33, one Sun Sparc 2, and one Sun Sparc 20. The computing power for each type of workstation is measured by the data to be used in the experiment. The results are listed in Table 2.
Table 2. The relative power of different workstations
|
Host |
Max. execution time |
Min. execution time |
Mean |
Relative power |
|
HP 715/33 |
101 secs |
96 secs |
97.86 secs |
1 |
|
Sparc 2 |
225 secs |
218 secs |
221.42 secs |
|
|
Sparc 10 |
110 secs |
103 secs |
105.3 secs |
0.929 |
|
Sparc 20 |
96 secs |
71 secs |
72.65 secs |
1.347 |
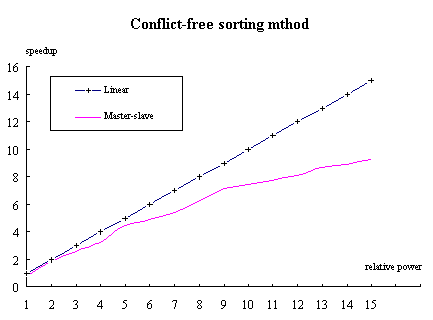
Figure 3. Speedup of the conflict-free sorting approach
A homogeneous computing environment composed of twelve Sun Sparc 2 workstations is formed. Two series of heterogeneous configurations are alsoconstructed which consists of up to 17 workstations of SPARC2, SPARC10, SPARC20/51. SPARC20/61 and HP715/33. The relative computing power of each different machine, as shown in Table 2, is measured by running the sequential version of the split-and-merge algorithm on every machine.
Table 2. The normalized computing power of different types of machines in the heterogeneous environment.
|
SPARC 2 |
SPARC 10 |
SPARC 20/51 |
SPARC 20/61 |
HP 715/33 |
|
|
Relative speed |
1.00 |
2.20 |
3.08 |
3.91 |
1.70 |
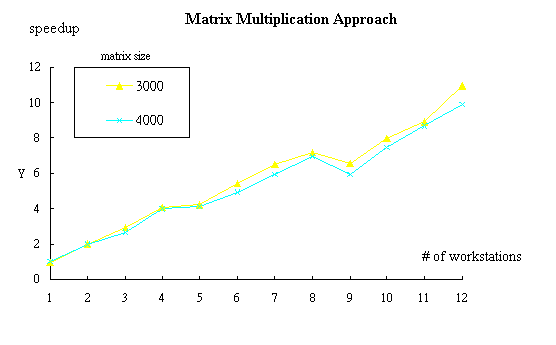
Figure 4. Speedup of the matrix multiplication approach
Generally, the rendering time in the virtual machine, we can be easy to give a simple formula : rendering time = computation time + communication time. In our application, The master process does not do the real computation and it is responsible for dynamically adjust the load So, the simple formula can not satisfy the physical evaluation. Then we propose a new analysis modeling, and the runtime considered are described blow:
T_host : The total execution time in the master process, from the first to the last executable line of the code.
T_data : The data manipulation time. It includes unpacking message, setting environment , getting configuration, … etc.
T_wait : The master process must wait the slave process for sending back the rendering result. So T_wait is the waiting time for slaves results.
T_comm : The communication time between the master and the slaves. Host to node communication time.
However, the analysis modeling of the master process section, it seems that it does not consist of computation time. In fact, when the master process assigns a new task to the slave process, it uses blocking receiving to wait for the rendering result. So, the computation time will be included in the waiting time T_wait. In this analysis modeling , T_host = T_data + T_wait + T_comm.
The total elapse runtime of a slave, T_slave_i, where i represents the slave number.
T_slave_i : The total execution time in the slave process, from the first to the last line of executable code.
T_data_global_i, T_data_local_i : The data manipulation time. It includes unpacking message, setting environment , getting configuration, … etc. But there is a little difference between T_data_global and T_data_local. It means T_data_local was calculated during the slave process manipulated its local data.
T_comp_global_i, T_comp_local_i : i-th slave processor computation time.
T_comm_master_i : Slave to host, host to slave communication time.
T_comm_slave_i : Slave to slave communication time.
T_idle_i : time the i-th slave spent in waiting for communications slave to slave, slave to master.
We have the following observations:
6. Conclusion
The experimental protocol has been proved to be an effective tool to characterize the performance of different applications of network computing. In this paper we have raised the issue of experimental protocol and designed a common protocol. From the protocol the experiments can be easily followed and performed. We have applied the protocol to the areas of matrix computation. Generally speaking, in the matrix computation problem, the speedup can be further improved if load balancing is adopted to distribute the work more evenly. Moreover, we observe that using fewer number of workstations but with larger normalized computing power has better speed performance than using a lot of workstations.
References
Appendix A : Source Code of Matrix Multiplication
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <time.h>
#include <sys/time.h>
#include <sys/types.h>
#include <math.h>
#include "pvm3.h"
#define SLAVE "multiply/grslave"
#define REQ 5
#define ACK 10
#define DATA 20
/*==================================*/
void main (ac, av)
int ac;
char **av;
{
/* Commom Vars */
int i, j, k;
int N, b1, b2;
float **A, **B;
struct timeval time, t1, t2, tt1, tt2;
int point;
float spawntime, sendtime, totaltime;
float cpt, mincpt;
struct slaveinfo{
int tid, power, RowS, RowE, grsize;
float ctime, speed, load;
} *slave;
/* PVM Vars */
int mytid, info, nhost, narch;
int id, dataflag;
struct pvmhostinfo *hostp;
/* Load Balance Vars */
int grsize;
/* EOVars */
/* Syntax Check */
switch (ac){
case 2:
N = atoi(av[1]);
b1 = b2 = N;
grsize = 1; break;
case 3:
N = atoi(av[1]);
b1 = b2 = N;
grsize = atoi(av[2]); break;
case 4:
N = atoi(av[1]);
b1 = atoi(av[2]);
b2 = atoi(av[3]);
grsize = 1; break;
case 5:
N = atoi(av[1]);
b1 = atoi(av[2]);
b2 = atoi(av[3]);
grsize = atoi(av[4]); break;
default:
puts("\n\t\tSyntax: stmain N <b1 b2> <GrainSize>\n");
puts("N\t: Matrix Size(NxN)");
puts("b1, b2\t: the bandwidth of Matrices\t(default: dense matrices)");
puts("GrainSize: Rows for each slaves to do\t(default: 1)");
exit(0);
}
/* printf("N=%d, b1=%d, b2=%d, GrainSize=%d\n", N, b1, b2, grsize); */
/* EOSyntaxCheck */
/* PVM Init & Configuations */
info = pvm_config(&nhost, &narch, &hostp);
if((nhost <= 1)||(info < 0)){
puts("\nNot Enough Hosts!!(Add More... ) or PVM not Running!\n");
exit(0);
}
/* pvm_catchout(stdout); */
mytid = pvm_mytid();
slave = (struct slaveinfo *)malloc(nhost*sizeof(struct slaveinfo));
printf("%dx%d %d nodes:\n", N, N, nhost-1);
/* EOPVMInit&Config */
/* Randomize */
gettimeofday(&time, (struct timezone*)0);
srandom(time.tv_usec);
/* EORandomize */
/* Allocate Matrix */
A = (float **)malloc(N*sizeof(N*sizeof(float)));
B = (float **)malloc(N*sizeof(N*sizeof(float)));
for (i=0;i<N;i++){
A[i] = (float *)malloc(N*sizeof(float));
B[i] = (float *)malloc(N*sizeof(float));
/* Assign Random Value */
for (j=0;j<N;j++){
A[i][j] = random()%5 + random()%5;
if ((j>i-b1)&&(j<i+b2))
B[i][j] = random()%5 + random()%5;
}
}
/* Print Matrix Value */
/* for (i=0;i<N;i++) { */
/* for (j=0;j<N;j++) */
/* printf("%2.0f ", A[i][j]); */
/* printf("\t"); */
/* for (j=0;j<N;j++) */
/* printf("%2.0f ", B[i][j]); */
/* puts(""); */
/* } */
/* EOPrintMatrix */
/* PVM Spawning Tasks */
/* Starting Time*/
gettimeofday(&t1, (struct timezone*)0);
for (i=1; i<nhost; i++) {
if (pvm_spawn(SLAVE, (char **)0, 1, hostp[i].hi_name, 1,
&slave[i].tid)!=1){
printf("Can't Spawn Task on host %s\n", hostp[i].hi_name);
for(j=1;j<nhost;j++)
pvm_kill(slave[i].tid);
i = 1;
info = pvm_config(&nhost, &narch, &hostp);
}
}
/* Waiting for slaves' Ack */
for (i=1; i<nhost; i++) {
pvm_recv(slave[i].tid, ACK);
/* printf("Slave %d in %s \n", slave[i].tid, hostp[i].hi_name); */
slave[i].ctime = slave[i].power = slave[i].load = 0;
slave[i].speed = hostp[i].hi_speed;
}
/* End Time */
gettimeofday(&t2, (struct timezone*)0);
spawntime = (t2.tv_sec-t1.tv_sec)+(t2.tv_usec-t1.tv_usec)/1000000.0;
printf("Spawn\t:%6.3f\n", spawntime);
/* EOSpawnSlaveTasks */
/* Init Slaves Before LB */
/* Starting Time*/
gettimeofday(&t1, (struct timezone*)0);
for(i=1; i<nhost; i++){
pvm_initsend(PvmDataDefault);
pvm_pkint(&i, 1, 1); /* Task Rank */
pvm_send(slave[i].tid, DATA);
}
/* End Time */
for (i=1; i<nhost; i++)
pvm_recv(slave[i].tid, ACK);
gettimeofday(&t2, (struct timezone*)0);
sendtime = (t2.tv_sec-t1.tv_sec)+(t2.tv_usec-t1.tv_usec)/1000000.0;
pvm_initsend(PvmDataDefault);
pvm_pkint(&N, 1, 1); /* Matrix Size(col) */
pvm_pkint(&b1, 1, 1); /* Matrix Band Width */
pvm_pkint(&b2, 1, 1);
pvm_pkint(&grsize, 1, 1); /* GrainSize */
/* Send Matrix B */
for(j=0; j<N; j++ )
pvm_pkfloat(B[j], N, 1);/* Pack Matrix B */
/* EOSendB */
/* Starting Time*/
gettimeofday(&t1, (struct timezone*)0);
for(i=1; i<nhost; i++){
pvm_send(slave[i].tid, DATA);
}
/* End Time */
for (i=1; i<nhost; i++)
pvm_recv(slave[i].tid, ACK);
gettimeofday(&t2, (struct timezone*)0);
sendtime += (t2.tv_sec-t1.tv_sec)+(t2.tv_usec-t1.tv_usec)/1000000.0;
printf("Send\t:%6.3f\n", sendtime);
/* Free Matrix B */
for(i=0; i<N; i++)
free(B[i]);
free(B);
/* EOInitSlaves */
/* goto free; */
/* Starting Time*/
gettimeofday(&tt1, (struct timezone*)0);
/* Load Balance Loop --- Fine Grain-- */
if(grsize>N){
grsize = 1;
puts("Warning! GrainSize > N! Resetting to 1.... ");
}
for(i=0; i<N; i+=grsize){
if((i+grsize) > N)
grsize = N - i;
/* printf("i=%d\tgrsize=%d\n", i, grsize); */
pvm_initsend(PvmDataDefault);
pvm_pkint(&i, 1, 1);
pvm_pkint(&grsize, 1, 1);
for(j=i; j<i+grsize; j++)
pvm_pkfloat(A[i], N, 1);
pvm_recv(-1, REQ);
pvm_upkint(&id, 1, 1);
pvm_send(slave[id].tid, DATA);
pvm_upkint(&dataflag, 1, 1);
if(dataflag>0)
for(j=slave[id].RowS; j<(slave[id].RowS+slave[id].grsize); j++)
pvm_upkfloat(A[j], N, 1);
slave[id].RowS = i;
slave[id].grsize = grsize;
slave[id].load += grsize;
}
/* Terminate Slave's LB Loop */
point = i;
for(i=1; i<nhost; i++){
pvm_initsend(PvmDataDefault);
pvm_pkint(&point, 1, 1);
pvm_send(slave[i].tid, DATA);
}
/* EOLBLoop */
/* Recv Slave Statistics */
for(i=1; i<nhost; i++){
pvm_recv(-1, DATA);
pvm_upkint(&id, 1, 1);
pvm_upkfloat(&slave[id].ctime, 1, 1);
}
/* EOSlaveStats */
/* End Time */
gettimeofday(&tt2, (struct timezone*)0);
cpt = (tt2.tv_sec-tt1.tv_sec)+(tt2.tv_usec-tt1.tv_usec)/1000000.0;
/* Show Times */
for(i=1; i<nhost; i++){
printf("%s comp time: %.0f rows in %3.5f secs ---> %5.0f\n",
hostp[i].hi_name, slave[i].load, slave[i].ctime,
slave[i].load/slave[i].ctime);
}
puts("_____________________________________________");
printf("Total: %6.3f\n\n", cpt);
/* Show Times */
/* Freeing Matrices */
free:
for(i=0; i<N; i++)
free(A[i]);
free(A);
free(slave);
/* EOFree */
pvm_exit();
exit(0);
}
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <time.h>
#include <sys/time.h>
#include <sys/types.h>
#include <math.h>
#include "pvm3.h"
#define REQ 5
#define ACK 10
#define DATA 20
/*=========================================*/
void main(ac, av)
int ac; char **av;
{
/* Commom Vars */
int i, j, k, l, m, n;
int N, b1, b2;
float **A, **B, **C;
float tm, cptime, sendtime;
struct timeval time, t1, t2;
/* PVM Vars */
int mytid, pid, rank;
int point, grsize, dataflag, load;
/* EOVars */
/* PVM Init */
mytid = pvm_mytid();
pid = pvm_parent();
/* EOPVMInit */
/* Sending Ack After Spawned */
pvm_initsend(PvmDataDefault);
pvm_send(pid, ACK);
/* EOSendACK */
/* Arrange Matrix */
pvm_recv(pid, DATA);
/* Sending Ack */
pvm_initsend(PvmDataDefault);
pvm_send(pid, ACK);
pvm_upkint(&rank, 1, 1); /* Task Rank */
pvm_recv(pid, DATA);
/* Sending Ack */
pvm_initsend(PvmDataDefault);
pvm_send(pid, ACK);
pvm_upkint(&N, 1, 1); /* Matrix Size(col) */
pvm_upkint(&b1, 1, 1); /* Matrix Band Width */
pvm_upkint(&b2, 1, 1);
pvm_upkint(&grsize, 1, 1); /* Grain Size */
/* Recieve Matrix B */
B = (float **)malloc(N*sizeof(N*sizeof(float)));
for(i=0; i<N; i++){
B[i] = (float *)malloc(N*sizeof(float));
pvm_upkfloat(B[i], N, 1);
}
/* EORecvB */
/* Allocate Matrix A & C */
A = (float **)malloc((grsize)*sizeof(N*sizeof(float)));
C = (float **)malloc((grsize)*sizeof(N*sizeof(float)));
for(i=0; i<grsize; i++){
A[i] = (float *)malloc(N*sizeof(float));
C[i] = (float *)malloc(N*sizeof(float));
}
/* EOAllocA&C */
/* goto free; */
/* Fine Grain Loop */
cptime = dataflag = 0;
/* REQ a Block */
pvm_initsend(PvmDataDefault);
pvm_pkint(&rank, 1, 1);
pvm_pkint(&dataflag, 1, 1);
pvm_send(pid, REQ);
/* EOReq */
while(1){
/* Recv a Block */
pvm_recv(pid, DATA);
pvm_upkint(&point, 1, 1);
if(point>=N)
break;
pvm_upkint(&grsize, 1, 1);
load += grsize;
/* Multiply A with B to C */
gettimeofday(&t1, (struct timezone*)0); /* Starting Time*/
for(i=0; i<grsize; i++){
for(j=0; j<N; j++){
C[i][j] = 0;
for(k=0; k<N; k++)
if((k>j-b2)&&(k<j+b1)) /* Band Condition */
C[i][j] += A[i][k] * B[k][j];
}
}
gettimeofday(&t2, (struct timezone*)0); /* Stopping Time */
tm = (t2.tv_sec-t1.tv_sec)+(t2.tv_usec-t1.tv_usec)/1000000.0;
cptime += tm;
/* EOMultiply */
dataflag = 1;
/* Pack Result */
pvm_initsend(PvmDataDefault);
pvm_pkint(&rank, 1, 1);
pvm_pkint(&dataflag, 1, 1);
for(i=0; i<grsize; i++)
pvm_pkfloat(C[i], N, 1);
/* EOPack */
pvm_send(pid, REQ);
}
/* EOFGLoop */
/*Send Slave Statistics */
pvm_initsend(PvmDataDefault);
pvm_pkint(&rank, 1, 1);
pvm_pkfloat(&cptime, 1, 1);
pvm_send(pid, DATA);
/* EOStatistics */
/* Free Matrix */
free:
for(i=0; i<grsize; i++)
free(A[i]);
free(A);
for(i=0; i<grsize; i++)
free(C[i]);
free(C);
for(i=0; i<N; i++)
free(B[i]);
free(B);
/* EOFree */
pvm_exit();
exit(0);
}
Appendix B : Source Code of Conflict-free Sorting Scheme
/******************************************************************/
/* To implement a parallel sorting method in the pvm flatform */
/* Using conflict-free single-channel sorting algorithm */
/* */
/* CIE of NSYSU */
/* Tainchi Lu */
/* 1997.4.23 */
/******************************************************************/
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <sys/times.h>
#include "pvm3.h"
#define MAXITEM 100
#define SLAVENAME "cfsort"
int LocalData[MAXITEM];
int DivTwo(int value);
void HeapTree(int NodeIndex, int bound);
main(argc, argv)
int argc;
char * argv[];
{
FILE *fp;
int mytid, myparent; /* process task id */
int child[MAXITEM];
int nchild, ndata;
int nhost, narch;
int value, rank;
int MsgTag_data, MsgTag_result, MsgTag_BroadcastSequ, MsgTag_broadcast;
int info, i, index;
int data;
int SortedData[MAXITEM]; /* sorted data are stored here */
char token[MAXITEM];
/* parameters in the child process */
int target, TotalData, node, temp, OtherSlaveNode;
int ParentNode;
int SequenceID, ChildNum;
int DataRank[MAXITEM], OtherSlaveData[MAXITEM];
int ChildID[MAXITEM];
int flag1, flag2, AddRank;
struct pvmhostinfo *hostp;
/* timing staff */
struct tms pbuf, tbuf;
struct timeval time1, time2;
long TotalTimeSec, TotalTimeMicrosec;
TotalTimeSec=TotalTimeMicrosec=0;
gettimeofday(&time1, (struct timezone*)0);
/* find out my task id number */
mytid = pvm_mytid();
if (mytid < 0)
pvm_perror("pvm_mytid");
/* find my parent's task id number */
myparent = pvm_parent();
if (myparent == PvmNoParent)
printf("I am the master, and my task id is %d\n", mytid);
if ((myparent < 0) && (myparent != PvmNoParent))
{
pvm_perror("pvm_parent");
pvm_exit();
}
/* To configure the pvm's environment */
pvm_config(&nhost, &narch, &hostp);
nhost=3*nhost;
/* define the message's flag */
MsgTag_data=1;
MsgTag_result=2;
MsgTag_BroadcastSequ=3;
MsgTag_broadcast=4;
/******************************************************************/
/* parent process */
/* if I don't have a parent then I am the parent */
/******************************************************************/
if (myparent == PvmNoParent)
{
/* To spawn the child processes */
nchild=nhost;
printf("To spawn %d child tasks in %d workstations\n", nchild, nhost);
info=pvm_spawn(SLAVENAME, (char **)0, PvmTaskDefault, "", nchild, child);
if (info == 0)
pvm_exit();
printf("Child process Task id : \n");
for (i=0; i<nchild; i++)
printf("%d ", child[i]);
printf("\n");
/* read the unsorted data */
fp=fopen("/home/users/tclu/work/sortdata.txt", "r");
if (fp==NULL)
{
printf("fopen failed\n");
/*exit();*/
}
index=0;
printf("Unsorted data : \n");
while (fscanf(fp, "%s", &token) != EOF)
{
data=atoi(token);
/* send the data to each child process by using interleave method */
pvm_initsend(PvmDataDefault);
pvm_pkint(&data, 1, 1);
pvm_send(child[index%nchild], MsgTag_data),
printf("%d ", data);
index++;
}
printf("\n\n");
pvm_initsend(PvmDataDefault);
data=-1;
pvm_pkint(&data, 1, 1);
pvm_mcast(child, nchild, MsgTag_data);
pvm_initsend(PvmDataDefault);
pvm_pkint(&nchild, 1, 1);
pvm_mcast(child, nchild, MsgTag_data);
fclose(fp);
/* to announce the child process to broadcast */
for (i=0; i<nchild; i++)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&child[i], 1, 1);
pvm_pkint(child, nchild, 1);
pvm_mcast(child, nchild, MsgTag_BroadcastSequ);
printf("To announce TID %d to broadcast\n", child[i]);
}
ndata=index;
printf("Sorting phase ............................................\n");
/* receive the sorted data from any child process */
for (i=0; i<ndata; i++)
{
info = pvm_recv(-1, MsgTag_result);
if (info < 0)
pvm_perror("pvm_recv");
pvm_upkint(&value, 1, 1);
pvm_upkint(&rank, 1, 1);
SortedData[rank]=value;
}
/* display the sorted data */
printf("Sorted data : \n");
for (i=0; i<ndata; i++)
printf("%d ", SortedData[i]);
printf("\n");
/* display the elapsed time */
gettimeofday(&time2, (struct timezone *)0);
TotalTimeSec = time2.tv_sec - time1.tv_sec;
TotalTimeMicrosec = time2.tv_usec - time1.tv_usec;
printf("The total elapsed time is %ld microseconds\n", TotalTimeSec*1000000+TotalTimeMicrosec);
pvm_exit();
/*exit();*/
}
/******************************************************************/
/* child process */
/* I'm a child */
/* The heap sort is adapted to sort the local data */
/******************************************************************/
if (myparent != PvmNoParent)
{
/* receive the data from the parent process */
TotalData=0;
target=0;
while (target != -1)
{
pvm_recv(myparent, MsgTag_data);
pvm_upkint(&target, 1, 1);
if (target != -1)
{
TotalData++;
LocalData[TotalData]=target;
}
}
pvm_recv(myparent, MsgTag_data);
pvm_upkint(&ChildNum, 1, 1);
/* using heap sort to sort the data */
node=TotalData;
ParentNode=DivTwo(node);
for (i=ParentNode; i>0; i--)
HeapTree(i, node);
for (i=node-1; i>0; i--)
{
/* swap the fist element and the i'th element */
temp=LocalData[i+1];
LocalData[i+1]=LocalData[1];
LocalData[1]=temp;
HeapTree(1, i);
}
/* define the rank */
for (i=1; i<=node; i++)
DataRank[i]=i-1;
/* broadcasting the local data to the other child processes */
for (i=0; i<ChildNum; i++)
{
pvm_recv(myparent, MsgTag_BroadcastSequ);
pvm_upkint(&SequenceID, 1, 1);
pvm_upkint(ChildID, ChildNum, 1);
if (mytid == SequenceID)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&node, 1, 1);
pvm_pkint(LocalData, node+1, 1);
pvm_mcast(ChildID, ChildNum, MsgTag_broadcast);
}
else
{
pvm_recv(SequenceID, MsgTag_broadcast);
pvm_upkint(&OtherSlaveNode, 1, 1);
pvm_upkint(OtherSlaveData, OtherSlaveNode+1, 1);
/* using merge sort and adjust the rank of local data */
flag1=flag2=1;
AddRank=0;
while ((flag1<=node) && (flag2<=OtherSlaveNode))
{
if (LocalData[flag1] <= OtherSlaveData[flag2])
{
DataRank[flag1]+=AddRank;
flag1++;
}
else
{
AddRank++;
flag2++;
}
}
if (flag2 > OtherSlaveNode)
for (i=flag1; i<=node; i++)
DataRank[i]+=AddRank;
}
}
/* send the result to the parent process */
for (i=1; i<=node; i++)
{
pvm_initsend(PvmDataDefault);
pvm_pkint(&LocalData[i], 1, 1);
pvm_pkint(&DataRank[i], 1, 1);
pvm_send(myparent, MsgTag_result);
}
pvm_exit();
/*exit();*/
}
}
int DivTwo(int value)
{
int quot, rem;
rem=value%2;
quot=(value-rem)/2;
return quot;
}
/******************************************************************/
/* heap sort */
/* to build the heap tree */
/******************************************************************/
void HeapTree(int NodeIndex, int bound)
{
int temp, MaxNode, LeftChild, myparent;
int done;
done=0;
MaxNode=2*NodeIndex;
while ((MaxNode <= bound) && (done == 0))
{
if (MaxNode < bound) /* to check the right child node */
if (LocalData[MaxNode] < LocalData[MaxNode+1])
MaxNode=MaxNode+1;
myparent=DivTwo(MaxNode);
if (LocalData[myparent] >= LocalData[MaxNode])
done=1;
else
{
temp=LocalData[myparent];
LocalData[myparent]=LocalData[MaxNode];
LocalData[MaxNode]=temp;
MaxNode=2*MaxNode;
}
}
}