當我們自個物件中取出個排列,一共會有n!/(n-m)!種排列的方法,如果我們依照lexicographic
order排列,如此就可以得到一個順序,有了順序之後,我們便可以要求要求出第幾種排列方法或是某一個排列方法的為多少。
我程式中用了兩種方法來求出所有的組合,一為
void GetPermByRank(int n, int m, char *ans, int rank)
表示 n 取 m 的時候,的排列為何,所得到的答案存放在ans中,如此便可以任意的取得某的排列。
另一個為
void GenerateNext(int n, int m, int rank, int num, char *ans)
表示取的時候,自起產生種組合,分成這兩種方法來產生,而不用GetPermByRank直接以迴圈產生所有的主要是因為直接計算某的組合,要比已知某組合,求其下一個組合要費時的多,所以只要先利用GetPermByRank取得起始點,在依序求出連續的num個組合,效率較高。
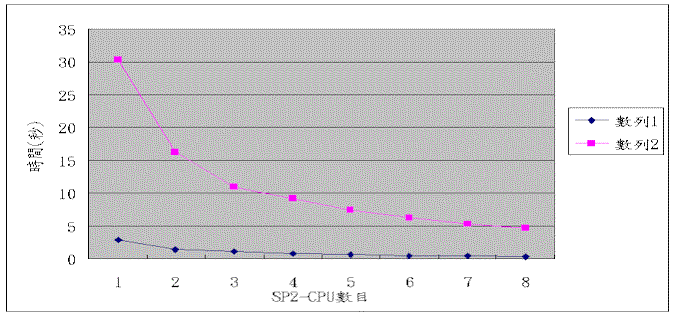
採用平行處理的時候,以vertical parallelism來作,例如 5 取 4 的時候,一共有 120 種排列方法,假設我們有 8 顆CPU,我們便分配每個計算 15 種排列,如此當每個做完的時候,便可得到完整的解,如此理論上所需的時間僅需要 1/CPU的總時間。
以下列出測試數據,所有的測試均至少取三次結果的平均,並捨棄差異過大的答案:
Pentium 200MMX (超頻至250) |
SP2 1CPU |
SP2 2CPU |
SP2 3CPU |
SP2 4CPU |
SP2 5CPU |
SP2 6CPU |
SP2 7CPU |
SP2 8CPU |
IBM6 | |
10P9(3628800) |
4 |
2.83 | 1.461.94ヾ | 1.112.55 | 0.783.63 | 0.614.64 | 0.565.05 | 0.466.15 | 0.407.08 | 12.59 |
11P10(39916800) |
19 |
30.32 | 16.361.85 | 10.952.77 | 9.253.28 | 7.384.11 | 6.214.88 | 5.345.68 | 4.616.58 | 127.99 |
此次測試的時間數據,均使用profile取得GenerateNext所花的時間,即為單存產生所有排列所需要花的時間,如此所取得的時間,和使用time函數取得的時間值差異跛大。

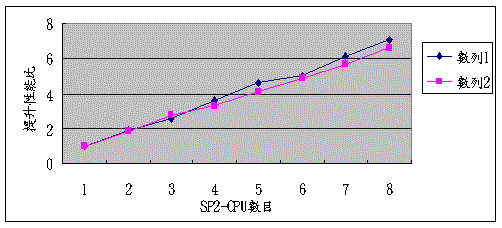 附註:
附註:
1.紅色數據表示與單所花的時間相比,效能為單運算的幾倍。