

國立中山大學應用數學系碩士班一年級
曾國尊
8624607
tsengkt@math.nsysu.edu.tw
前言:
矩陣相乘的題目,由於受限於
CPU的數目,在此我們比較的個數分別為1、2、4、8顆CPU,觀察是否在CPU增加時,其時間能夠相對減少?理想是在CPU個數增為兩倍時、時間能減至二分之一!但是我們事前已然知道、CPU彼此間的通訊也花時間,因此該當是不能達到一個COST=CPU×TIME的理想狀況,此實驗的目的在於看出其通訊時間的影響。方法:
我們採用的方式乃是很一般的方式,純粹是使用
O(n3)的sequential演算法,將資料平均分配給各個CPU去各自運算,最後寫出總和即是,程式的原始碼我們附於最後、以資參考。實驗結果:
初看
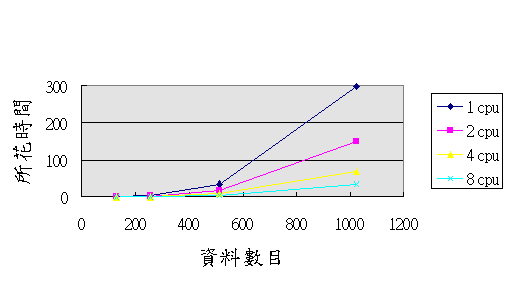
由上圖,明顯地、我們可以看出
CPU個數的增加可降低時間的花費!然而是否CPU增倍、時間亦可減半?上圖中可能不盡詳細,以下我們列出數據參考、分析。說明:
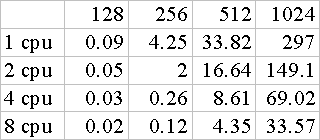
首先我們說明一下上表內容,
(4 cpu, 512, 8.61) 表示用四顆cpu去做512x512的矩陣相乘時,花費時間為8.61秒。在此我們時間的取得是筆者將同樣的資料數跑三次、取得三次時間中、最小的時間!(筆者以為如此才”接近”最佳時間)同時、在每次的時間中、例如四顆cpu各自花了不同的時間,我們則是在四者中取最長時間來當作工作執行的時間。另表:
考慮上表可能亦不是很好看,我們將
8CPU所花的時間做為基數、比較1、2、4顆CPU在不同資料數中各花多少時間基數?
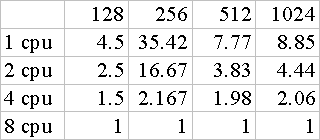
理論上,時間基數不管矩陣大小為多少,都該是
1CPU花八個時間基數、2CPU花四個時間基數、4CPU花兩個時間基數,這樣方可符合前言中提出之COST=CPU×TIME。而且因為是將8CPU做為時間基數,此時間基數中已然包含了通訊的耗費時間,而在較少顆CPU時、所花的通訊時間該當較少,因此按理會比上述的理論時間基數尚少些、而且該是有少無多。以下我們討論上表:
由表我們可以觀察到在矩陣大小為
128×128時,運算量較少、通訊亦無多,會有這樣的數據出現、筆者以為是合理的!或者有人會有疑問、為什麼時間基數比之預期少了那麼多?筆者以為這乃是由於資料量少、花費時間過少而無法準確偵測花費時間、精確度不夠的關係,就是這樣子。
然而上表中
256×256卻是個極不合理的情形,按理時間基數有少無多,而在此欄中卻是多的離了譜,筆者曾想可能是當時系統的CPU尚有別的工作之故,但在不同時間的三次裡、於256×256的矩陣中、卻一而再、再而三地出現這種數據!筆者無奈、只得照實寫出。也許我們把這個當作是一個錯誤吧…
接下來的一欄是個完美的結果、與我們的推測完全符合,而且亦是
CPU個數愈少、離理論時間基數愈遠,這是因為通訊耗時愈少的緣故。故筆者以為在理論上的結果中、512×512的矩陣大小、是一個良好的測定值。
後來我們看到了反其道而行的
1024×1024,它離我們想像中的時間基數是相去不遠!可是在想法中,與理論相比該是有少無多、然而在此欄中卻是有多無少,為什麼?筆者仍舊以為這是合理的,因為此時我們的資料已到達1024×1024,這是個頗大的資料量!故此時運算力的需要已超過通訊時所花費的時間了!所以在比較上、離我們想像的時間基數有一點差距!
筆者以為資料再大下去的話、應該會同這一欄的情形差不多!即是與時間基數相去不遠、但比之理論時間基數該是較高的情形!不過由於接下去的資料量實在太大、筆者並未測試、一切純屬推測!
結論:
本來筆者預期關於通訊耗時之事、在資料量變大之時,情況會更加嚴重!亦即筆者以為在很大的資料量時,一顆
CPU所花的時間、比之八顆CPU,定然不到八倍!然我們可以看出這個想法在矩陣大小為1024×1024被推翻!在筆者細思之後,筆者以為通訊的增長情形為O(n2logN),然運算力的增長情形則為O(n3),(N為CPU個數,n為矩陣大小),故在資料量增長到某個界限以上時、通訊的時間就可能被忽視而不影響了。
附件:
#include <mpi.h>
#include<stdio.h>
#include<stdlib.h>
#include<sys/timers.h>
/*
嗯,上面這一些話該當不用寫註解才是…*/
main(int argc, char **argv)
{
int NN,i,j,k,a[N][N],b[N][N],c[N][N],d[N][N];
/*
計畫中是做矩陣相乘, axb=c ,因此上面要了 a、b、c 三個 NxN 的矩陣…*//*
而 d 矩陣是為傳輸資料用的暫存矩陣,i、j、k 為 loop 所使用…*//*NN
是每個 cpu 所分得的資料量…*/
int ind,indd,me,procs,ntag=100;
/*ind
、indd 各為各個 cpu 做相乘時的開始及結束點…*//*me
為 cpu 編號,procs 為 cpu 使用之個數,ntag 純粹為配合函數使用…*/
MPI_Status status;
time_t start,end;
/*start
、end 記錄起始時間、結束時間…*/
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &me);
MPI_Comm_size(MPI_COMM_WORLD, &procs);
/*
做初始化的動作、並取得 cpu 編號及個數…*/
srand(N);
/*
為將造出的矩陣做亂數初始的動作…(
本來是用「時間」做亂數種子,但發現各個 cpu 的資料產生不同的矩陣!奇怪的是在上回的 bitonic sort 時,產生的亂數是八顆皆相同,因為按理它們是八顆「同時」做亂數初始才是,但結果這回做卻是八顆並不同步!為免造出的矩陣仍得做資料傳輸,因此拿 N做為亂數種子,以方便進行)*/
NN=N/procs;
/*
計算每個 cpu 需負擔多少個資料…*/
for(i=0;i<N;i++)
for(j=0;j<N;j++)
{
a[i][j]=rand()%2;/*
產生 a 矩陣*/b[i][j]=rand()%2;/*
產生 b 矩陣*/
/*
因在測試中可能使用極大的矩陣以測出時間,故我們用以相乘的矩陣其元素只有 0 與 1,如此便不會超出 int 的範圍…*/
c[i][j]=0; /*
起始 c 矩陣*/d[i][j]=0; /*
起始 d 矩陣(暫存用)*/}
time(&start);
/*
取得起始時間…*/
ind=me*NN;indd=ind+NN;
/*
計算各個 cpu 在矩陣計算中的起始及結束位置…*/
for(i=0;i<N;i++)
for(j=0;j<N;j++)
for(k=ind;k<indd;k++)
c[i][j]+=a[i][k]*b[k][j]; /*
各個 processor 算出各自的 c 矩陣*/for(i=1;i<procs;i*=2)
{
if((me+i)%(2*i)==0)
MPI_Send(c, N*N, MPI_INT, me-i, ntag,
MPI_COMM_WORLD); /*
該送出資料的 processor 送出資料*/else if(me%(2*i)==0)
MPI_Recv(d, N*N, MPI_INT, me+i, ntag,
MPI_COMM_WORLD, &status); /*
該接收的 processor 接收資料*/if(me%(2*i)==0)
for(k=0;k<N;k++)
for(j=0;j<N;j++)
c[k][j]+=d[k][j]; /*
收到資料的 processor 處理資料*/
/*
將傳來的資料給加到原來的 c 矩陣中…*/
}
time(&end);
/*
計算結束,取得結束時間…*/
if(me==0)
printf("Matrix %dx%d with %d processor(s)\n",N,N,procs);
printf("Total time:%d\n",end-start);
/*
印出相關資料及時間…*/
MPI_Finalize();
return(0);
/*
ㄟ~~,戲完了、可以散場了…*/
}
/*
我們並沒有印出計算的結果,那不重要,不過答案真的是對的啦,^_^*/