The Report of Term Program of Parallel Algorithm
平行演算法期末程式報告
題目:平行的快速排序法(Parallel QuickSort)
黃國璽
國立中山大學應用數學系碩士班一年級
1.平行的快速排序演算法
簡而言之,平行的快速排序法就是先將資料分幾個部份,同一個部份中的資料都比前一個部份的每一個資料大,反之亦然。接下來再就每個部份進行快速排序法,而快速排序法(qsort())在C程式已經是個被內建的函數,可以加以利用。
假設目前我們有n個處理器,如果我們不考慮處理器間資料傳輸的時間以及將資料切開的時間,那平行的快速排序法將會比沒有平行快上n倍,也就是說,所花費的時間將為原來的1/n倍。可是實際上,將資料分類以及處理器的溝通都是要花費時間的。
我們都知道快速排序法會因為選取的基準數而影響所花費的時間,時間複雜度是介於O(n logn)到O(n2),平行的快速排序法因為最後也是執行快速排序的工作,所以也會有快速排序法所有的特性。
我們在切割資料的過程中選取的切割點也會影響整個程式的表現,如果能夠平均地將資料分開,那表現將會最好,如果運氣不好,大部分資料都分在同一個部份,那整個平行的快速排序將會與不平行的狀況幾乎一樣。
(1)實驗環境:IBM SP2
(2)程式執行結果:
由於切割的基準數與快速排序的基準數不是選取最佳的,所以程式的執行結果只能當作參考,但大體而言我們還是能從得到的實驗數據中觀察到一些大概的情形與結果。
在提供1000000個數字待排序的數列狀況下,我們得到了以下的實驗數據:
表一
|
CPU個數 |
CPU編號 |
程式執行時間 |
資料傳送時間 |
|
1 |
0 |
11 |
0 |
|
2 |
0 1 |
12 12 |
4 7 |
|
4 |
0 1 2 3 |
14 14 14 13 |
13 13 6 11 |
|
8 |
0 1 2 3 4 5 6 7 |
21 19 21 21 21 21 21 20 |
20 17 21 21 21 19 21 10 |
在執行proc分析後到以下的數據:
表二
|
CPU個數 |
CPU編號 |
CPU執行時間 |
|
1 |
0 |
8.72 |
|
2 |
0 1 |
5.35 2.38 |
|
4 |
0 1 2 3 |
1.99 1.23 3.25 5.20 |
|
8 |
0 1 2 3 4 5 6 7 |
4.74 1.00 1.59 0.98 3.05 4.37 3.38 2.62 |
為了能更能了解以上數字間的關係與意義,我們將以上的數字畫成以下的圖表:
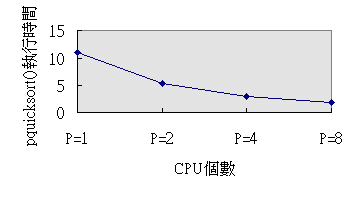
圖一依據表一的數據,將程式執行時間減去資料傳送(包含等待)的時間,再取平均值。

圖一
CPU個數與程式執行時間
圖二依據表二的數據,將CPU時間取平均值作圖。
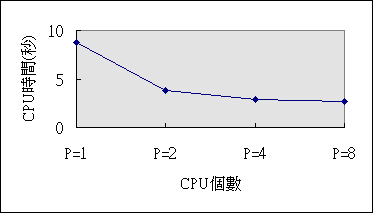
圖二
CPU個數與花費的CPU時間
由圖一可以粗略地看到隨著CPU個數的增加,程式執行時間依照CPU個數遞減。雖然圖二也看到了花費的時間隨著CPU個數的增加而遞減,但是遞減幅度逐漸減少,造成這個現象最主要的原因在於CPU除了原來排序的工作之外,另外還要負責將資料分類的工作,而將資料分類隨著CPU個數增加,工作的層數和複雜度也隨之增加。
依據Kaijung Chang, yan Huat Tan, Yaakov Varol, Jiang-Hsing Chu的論文”An Optimal In-Place Parallel Quicksort”,這個程式所採用的平行快速排序演算法的時間複雜度為O((n/p)log n + (n/p) (log p)2),n為輸入資料的大小,p為處理器的個數。
3.結論
說實話,MPI的程式並不是很好寫,要先將資料傳送的來源與目的地確定之後才能將程式寫對,寫程式的除錯過程中往往錯誤都發生在資料傳送的階段。另外,由於IBM SP2不是Shared Memory的架構,對於平行的快速排序法而言就必須花費額外的資料交換才能確保每個處理器間的資料同步,在確保資料同步的前提下,先完成工作的處理器就必須要等待相關的處理器完成工作後把資料加以交換,如果分配的資料量不均,就要等到相對的部份完成後才能繼續下面的步驟與工作,整個程式的表現多少被這個原因給拖了下來。
程式原始碼