Faster Fourier transforms 在單CPU中是以divide-and-conquer的方法，在多CPU的版本中也是以這個方法做。先以一個Node隨機產生一組數據，在這個程式中取65536個複數，然後將這些數據平均分配給所要執行的Node﹙在這個程式中為1、2、4或8個Node﹚，每個Node各自用divide-and-conquer的方法算出所分配到數據的FFT，然後將結果merge，就可以得到這65536個數據的FFT。

測試環境：

以ibm26和SP2比較單CPU和多CPU的效能，因為在SP2上每個Node的效能相差蠻大的，所以在測試一個Node以上的效能時以所有Node的平均時間來代表這次的執行時間。在這個測試中用兩種方法計算時間，一種是以profile計算出CPU的執行時間，另外用一個function MPI_Wtime()來計算實計執行時間，在執行時Node1因為不明原因使得執行時間比其他的Node多出快一倍。使用MPI_Wtime()計算時間已經去掉了產生數據的時間，所以Node0的load不會比其他Node重。

下面是這個程式的測試結果：

By profile：

Figure. 1

By MPI_Wtime：

Figure. 2

由以上的數據發現Node個數愈多，所得到的效果愈少，這是因為這個程式是由一個Node產生數據再分給其他Node，所以會造成某些Nodes需要等待，而且merge的時候也會使得某些Nodes等待。

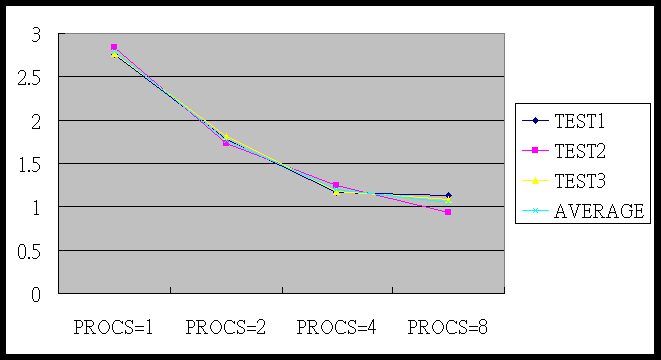
圖表：

這個圖是由figure 1的數據所畫成的，可以看出由procs=1 到 procs=2時，運算速度約快1.6倍，由procs=2 到 procs=4，速度約快1.5倍，而由 procs=4 到 procs=8，速度只增加1.14倍，可以說是沒有增加多少效能，可能是因為測試的數量不夠大，所以增加的效能被傳輸時間抵消掉了。