Odd-Even Merge Sort 測試報告

8624618 陳嘉智

　　˙單CPU版程式

　　˙多CPU版程式

　　˙測試機器︰ IBM SP2 (140.117.2.17)

　　˙測試方法： Compilier 時加入 -O -p 的參數，執行完執行檔後執行 prof 分析，

　　　　　　　　 找出做 Odd-Even Merge Sort 部份的時間記錄下來。

　　˙測試數據： 以秒為單位

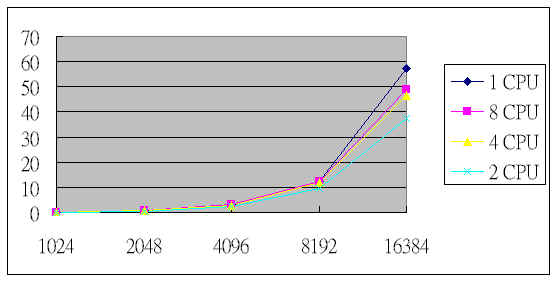
數列長度 單CPU 8 CPU 4 CPU 2 CPU
1024 0.19 0.19 0.19 0.16
2048 0.76 0.77 0.97 0.56
4096 3.03 3.02 2.92 2.32
8192 12.25 12.18 12.01 9.35
16384 57.36 48.77 46.55 37.41

上圖中，直的部份為時間(秒)，橫的部份是數列長度

　

　　˙測試結果： Odd-Even Merge Sort 在一顆CPU下的時間是 O(log2n)，而在多 CPU

　　　　　　　　 時我採用的方式是先把數列分成 (CPU數目) × 2 等分，每顆 CPU

　　　　　　　　 各別存取兩等分，然後把每等分的數列看成是單CPU版中的一個

　　　　　　　　 數，利用單CPU版中四個數 sort 的方法，一次拿兩顆CPU裡的數

　　　　　　　　 列 sort ，而sort 完後再把 sort 好的數列全部丟到兩顆CPU中編號較

　　　　　　　　 小的一顆，以 Tree 的方式進行。

　　　　　　　　 以 8 顆CPU為例，第一次是編號 0 跟 1，2 跟 3，…，6 跟 7 兩兩

　　　　　　　　 sort 後把 sort 好的數列分別丟到編號 0，2，4，6 的CPU，然後第

　　　　　　　　 二次是編號 0 跟 2，4 跟 6 比完後分別丟到編號 0，4 的CPU，第

　　　　　　　　 三次類推。

　　　　　　　　 這樣的方法使用的CPU數會漸漸變少，所以只有在 2 CPU時才能

　　　　　　　　 算是真正的平行，而如數據所見，8 顆CPU 的速度只比單顆CPU

　　　　　　　　 快一點，是因為在做最後一次 sort 時， sort 的數列長度是原本數

　　　　　　　　 列長度的一半，加上前面 sort 所花的時間總和，也就是要花 ：

　　　　　　　　 (數列長度/2)的時間 ﹢(數列長度/4)的時間 ﹢(數列長度/8)的時間

　　　　　　　　 這樣所花的時間跟直接 sort 整個數列的時間相比雖然有見少，但

　　　　　　　　 也相差不遠，而 4 CPU 所花的時間：

　　　　　　　　 (數列長度/2)的時間 ﹢(數列長度/4)的時間

　　　　　　　　 比 8 CPU 少了 (數列長度/8)的時間 的部份，只有 2 CPU 時是真正

　　　　　　　　 用到所有的 CPU，4 CPU 跟 8 CPU 的部份只能算是一半的平行而

　　　　　　　　 已，因為在單顆 CPU 裡用 recusive 的部份在多 CPU 裡要平行處理

　　　　　　　　 的關係，在找不到較好的關係式下所以採用這種不是完全平行的

　　　　　　　　 方法做，但若是只針對 8 CPU 或是 4 CPU 的平行計算而寫出相對

　　　　　　　　 的程式，應該會有比這種用 Tree 的方法還要好的結果。