題目:Gauss-Jordan消去法平行程式測試報告
課程科目:平行演算法
任課老師:楊昌彪
學生:紀智超
簡介:
單CPU的做法為:
將線性多項式(Linear Equation)的係數代入一增廣矩陣中,以Gauss-Jordan消去法將此增廣矩陣化為對角線矩陣(但最後一行元素不一定為零),則每列最後一行元素除以同列對角線元素即為多項式之解.演算法:
procedure SIMD GAUSS JORDAN (A,b,X)
step 1:
for j=1 to n do
for i=1 to n do
for k=j to n+1 do
if (i<>j) then
a[i][k]=a[i][k]-(a[i][j]/a[j][j])*a[j][k]
step 2:
for i=1 to n
x[i]=a[i][n+1]/a[i][i]
多CPU的做法為:
在step1的for i=1 to n 的迴圈上,依(i mod cpu使用個數)所得值,決定交由那顆CPU處理迴圈內的程式,再由第1顆CPU負責傳送執行結果,以確保各CPU的矩陣是相同且正確.最後各CPU將化為對角線矩陣傳回第1顆CPU,由第1顆CPU執行step2.
程式:
測試數據:
單CPU版:
| MachineType |
n=2 |
n=4 |
n=6 |
n=8 |
n=10 |
n=20 |
n=30 |
n=40 |
| PC(120HMz) |
0.000110 |
0.000549 |
0.000154 |
0.000341 |
0.000626 |
0.004352 |
0.014176 |
0.032692 |
| IBM |
0.000005 |
0.000035 |
0.000103 |
0.000213 |
0.000385 |
0.002890 |
0.009376 |
0.023 |
| SP2 |
0.000003 |
0.000014 |
0.000042 |
0.000091 |
0.000164 |
0.001105 |
0.003533 |
0.008086 |
| n=50 |
n=60 |
n=70 |
n=80 |
n=90 |
n=100 |
n=200 |
n=300 |
n=400 |
n=500 |
| 0.27203 |
1.08791 |
1.70879 |
|
|
|
|
|
|
|
| 0.04454 |
0.07722 |
0.11907 |
0.1806 |
0.2564 |
0.3494 |
2.823 |
8.668 |
20.58 |
40.14 |
| 0.01546 |
0.02637 |
0.04161 |
0.0618 |
0.088 |
0.121 |
0.9486 |
3.221 |
7.599 |
14.786 |
n : n為欲解變數的個數,則增廣矩陣大小為(n*n+1)
MachineType:測試時使用的機器
註:由於DOS記憶體的限制,PC的測試數據只到n=70
註:時間單為秒
多CPU版:
| Processor |
n=2 |
n=4 |
n=6 |
n=8 |
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
n=60 |
n=70 |
n=80 |
n=90 |
n=100 |
n=200 |
| 2 |
0 |
0 |
0 |
0 |
0 |
2.0 |
4.0 |
10.0 |
16.0 |
19.0 |
21.0 |
23.0 |
29.0 |
30.0 |
225.0 |
| 4 |
0 |
0 |
1.0 |
1.0 |
1.0 |
3.0 |
10.0 |
18.0 |
28.0 |
35.0 |
65.0 |
78.0 |
95.0 |
118.0 |
432.0 |
| 8 |
0 |
0 |
0 |
1.0 |
1.0 |
3.0 |
9.0 |
15.0 |
24.0 |
36.0 |
49.0 |
65.0 |
75.0 |
93.0 |
367.0 |
n : n為欲解變數的個數,則增廣矩陣大小為(n*n+1)
Processor:測試時使用sp2的CPU個數
註:由於n = 300 ~ 500 多CPU版所花時間過大,因此不不予測試
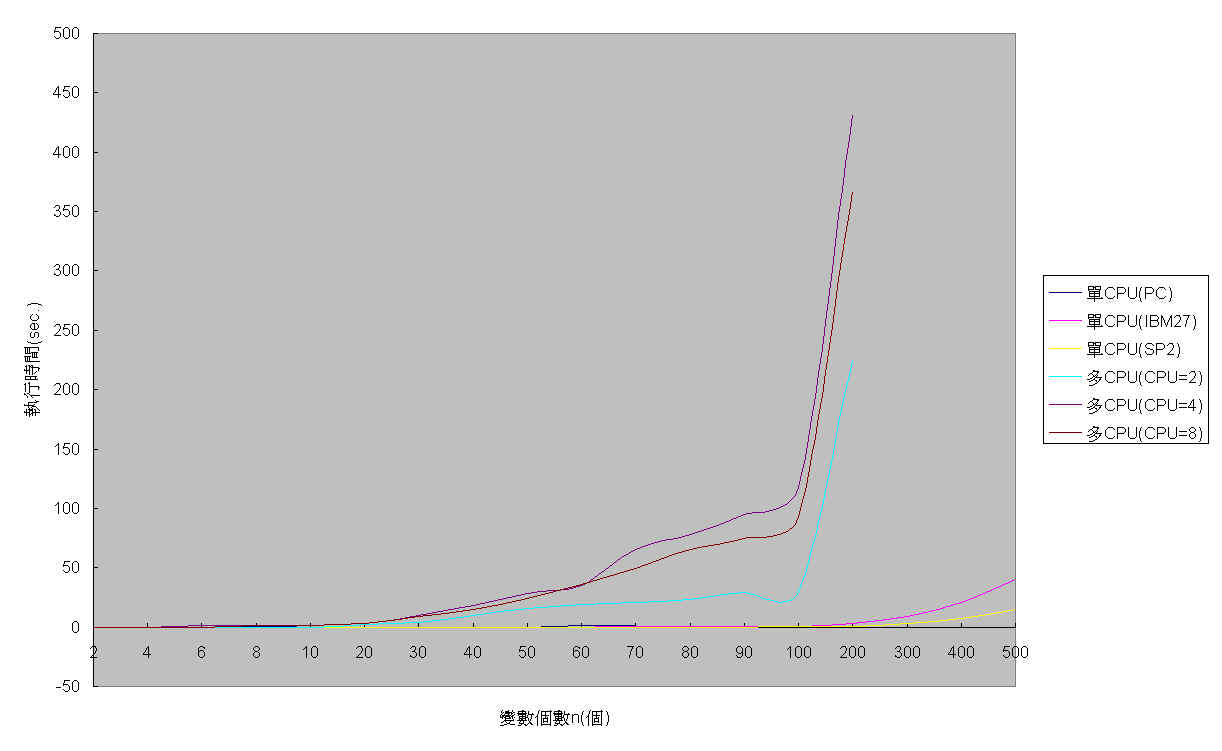
結論:
單CPU程式執行時,
每當 n 增加 2 倍時,則執行時間約增加 8 倍,當 n
增加 3 倍時,則執行時間約增加 27 倍........類推,當
n 增加 k 倍時,則執行時間約增加 k^3 倍(當 n
越大情形越顯著).頗符合演算法的時間複雜度O(n^3).而程式的瓶頸大多集中在矩陣的運算上,並無其他額外較大的消耗
(overhead)存在.
多CPU程式執行時,
增加倍數大約以n^2的倍數成長,但基本上都比單CPU執行時大上百倍以上,實際上都是受到CPU間傳輸時間影響,而此時間複雜度恰好為O(n^2),而此傳輸時間的成長速率已遠大於平行後節省的時間.因此降低CPU間傳輸時間或由傳輸時間較低的機器執,才可真正達到平行的目的.

