平行演算法期末報告
Huffman coding
國立中山大學應用數學系碩士班一年級
張震達
8724617
changjd@ibm7.math.nsysu.edu.tw
動機 :
之所以會選這個題目,我想它的來由就是...,廢話不多說,所以當我決定要做這個題目時,直覺反應是它有哪些地方可以被平行化? 想不通,所以去找看看是否有這方面的paper,很可惜的是沒找到所想要的paper,所以就只好問問別人和自己想想看是否有好的方法了。
實作方法:
基本上,直覺反應在建構tree時很難去平行化,應該是有方法,只是我沒想到罷了,再加上自己考量會用到的符號應該不會超過255個,所以就把平行化的重心放在計算各個符號之頻率。而我的作法是每個CPU個自去計算在它自己內的每個符號出現之頻率,然後再將計算結果傳到一個CPU(在自己的程式內是第0號CPU),累加各個符號的頻率得到每個符號出現之所有頻率後,最後再在此CPU上做建構tree則即完成本程式。
另外,原本是考量各個CPU對欲coding之檔案作分割然後個別讀取檔案內容,後來在寫好之後測試,發現到當檔案很大時,I/O會影響到計算的時間,所以後來就改版成各個CPU用亂數產生符號,然後計算每個符號之頻率。
執行結果:
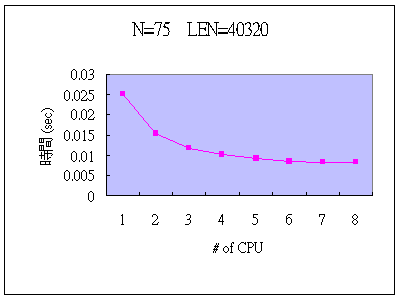
N=75 (會出現的符號之個數, 由0 (Dec 值為 48) 到 z (Dec值為 122) )
LEN=40320 (欲coding 之文字長度,40320=1*2*3*4*5*6*7*8 )
| # of CPU | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Time | 0.025097 | 0.015497 | 0.0117566 | 0.0102273 | 0.0092523 | 0.0086053 | 0.0084583 | 0.00819967 |
說明:上表的資料是Run三次的結果取平均值,我們也可以由上表的資料明顯的看出當CPU個數越多,程式執行時間也相對的越少,與理論和推測相符合,再由下兩表更可以明顯看出其效果。
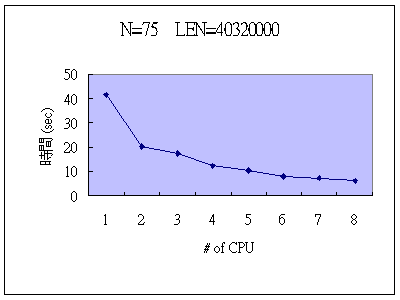
N=75, LEN=40320000 (Run三次取平均值)
| # of CPU | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Time | 41.65631 | 20.48742 | 17.20463 | 12.47761 | 10.45706 | 8.22231 | 7.12300 | 6.13203 |
說明:由上表我們可以看出單個CPU和2 個CPU執行結果差兩倍,而單個CPU和8個CPU執行結果差了6.7932倍,由此可知對於2 個 CPU而言,其執行結果提升了兩倍是很理想的,而後來8 個CPU之所以效果沒有提升至8倍,主要原因應該是受到訊息傳遞的影響所以才只提升了6.7932倍。故由此可知當資料量越大時,訊息傳遞的時間會影響到計算時間。
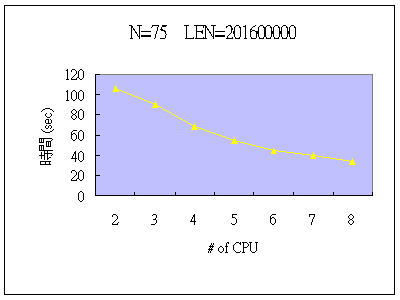
N=75, LEN=201600000 (201600000 = 40320*5000, Run三次取平均值)
| # of CPU | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Time | 無法執行 | 106.21976 | 90.13014 | 68.47756 | 54.15564 | 44.66882 | 39.28789 | 34.27537 |
說明:上表的單個CPU內會有無法執行的原因,經過測試,應該是因為單個CPU無法配置如上面 LEN量多之記憶體,而多個CPU 則因為平均分配,而每個CPU 動態配置記憶體的量較少,故可以成功地執行。
以下為上述各表之曲線圖:

結論:
由這次結果我們可以知道,當要處理的資料量越大時,使用越多的CPU 來處理固然可以增加執行效率,不過同時也要考慮各個CPU 間的訊息傳遞所需的時間,因為訊息傳遞的時間會使得結果不如預期來的理想,甚至會影響真正要處理資料的時間,而把大多時間花在彼此的訊息傳遞上,這樣所得的效益是不大的。
附上:Source Code