圖1
資工所博士班一年級 吳志峰 9034811
所謂的Steiner tree problem[1,2,3]是指在一無向圖G(V,E)中, 給定一組V的子集合S, 我們要在其中找到一個 minimum cost tree, 這個 tree 必需包含S中所有的點, 另外也可包含一些非S中的點。這些非S的點我們稱之為 Steiner nodes, S中的點我們稱之為 terminals。
Steiner tree problem 是屬於 NP-complete 的間題, 代表著我們目前找不到一個 deterministic 的演算法, 能夠在polynomial 的時間內解決這個問題, 但是還是有演算法可以在 exponential time O(N) or O(M) 解決這個問題, 其中|V|=N, |S|=M。以下是這個問題的一些可能解法[3]
Topology Emumeration algorithm. 找出 W 中所有可能的minimum spanning tree, W為V的子集合並且包含S, 在這個方法中會有 2^(N-M) 的 W 來試驗.
令 CR = T algorithm / T optimum
The Shortest Path algorithm. 從 S 中找出任意一個點, 從這個點建立一個 shortest path tree 到其它所有的點, 再將這個tree 中指到非 terminal 多餘的 edge 刪除。此演算法的 time complexity 為 O(N^2), 而 CR 為 O(M)。
The Greedy Algorithm. 從 S 中的任意一個點開始, 找出離目前所建構出的的 tree 最近的 terminal, 並將它加到 tree 中, 重複這個步驟一直到所有的 terminal 全部加進來為止。此演算法的 time complexity 為 O(M*N^2), 而 CR <= 2。
The Kou Markowsky and Berman algorithm (KMB), 本次報告所使用的演算法為此一方法, 容詳述於後。此演算法的 time complexity 為 O(M*N^2), 而 CR <= 2。
實驗所作出的結果大致和其time complexity吻合,即 N 加偣, 時間就多花上4偣的時間, 而 M 越大所需的時間也呈現線性增加。

圖1
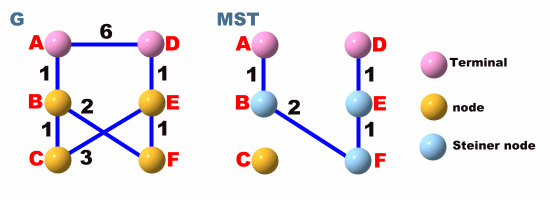
所謂的 Steiner Tree Problem, 是一組無向圖G(V,E)中, 給定一組 terminals, 如圖一的A和D, 然後我們必需在G上找到一個 minimum spanning tree, 這個 tree 必需滿足下面要求
在圖1中我們可以知道, 如果不能包含非 terminal 的點, 則找出來的 spanning tree, cost為6, 而且有可能根本找不到這樣的 tree, 在包含了一些 steiner node 之後, 所找出的 cost 為5。
The Kou Markowsky and Berman algorithm
Input: a undirect graph G(V,E) and a subset S of V.
Output: The minimum cost Steiner tree T.
Step1: 建構 distance graph G1(S, E').
對每一個 E' 中的 edge (u, v), 它的 cost 等於 G 中 u 到 v 的最短路徑的cost
Step2: 找出 minimum spaning tree T1 of G1
Step3: 建構 G2(V'', E''), 將T1的每一個 edge (u, v), 用它在Step1中所找的路徑代入.
Step4: 將G2中的cycle去掉.
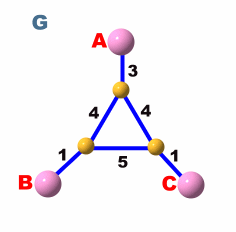

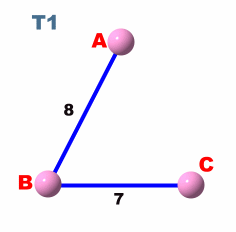



圖2
如圖2所示, 首先我們先建立一個包含所有 terminal 的 complete distance graph G1, 然後找出它的 minimum spanning tree T1, 然後將原路徑代回, 得到 G2, 最後將 G2 的 cycle 移去, 得到 total cost 為14 的 Steiner Tree T. 因為此一演算法為approximate algorithm, 所以它得到的steiner tree並一定都是optimum, 此例子的minimum Steiner tree的 cost 為 13。
此演算法的 time complexity 為 O(M*N^2), 而 CR <= 2。
在 step1 中必需建構一個distance graph, 在這裏我不採用 all shortest path algorithm, 因為大部份的 graph中, terminal 的數目均遠小於 |V|, 所以改採由每一個 terminal 建立一個 single source/all destination的shortest path tree, 在這裏所使用的演算法為 Dijkstra's algorithm。
在 step2 中需要建立minimum spanning tree, 這裏使用的方法為 Kruskal's algorithm, 在 Kruskal's algorithm中一個比較麻煩的地方在加入一個新的 edge 是否產生 cycle, 原本用的方法 tree traversal 的方法, 但是效果很差, 在 node 數在500左右時就跑不太動了, 後來改用 weighted union[4]的方法, 問題立刻解決。
在 step3 中要將原來的 path 代入, 由於在 step1中已經有為每一個 terminal 建立 shortest path tree, 所以可以很快的代入。
在 step4 中要將 cycle 移去, 在這裏我用了二個步驟, 第一步是去找 G2 的 minimum spanning tree, 第二步是用 tree traversal 的方式, 將 leaf 為非 terminal 的 edge 移去。
機器設備: AMD Duron 700 超頻到 800, RAM 640 MB
作業系統: Window XP
編譯器: Visual C++ Enterprise, Win32 console
本次實驗所使用的實驗資料為 SteinLib Testdata Library 所提供的測試資料, 它最大的好處是每一個測試資料都有提供Optimum solution的值, 以作為比較.
|
Name |
|V| |
|E| |
|T| |
Opt |
KMB |
TIME(ms) |
|
c01 |
500 |
625 |
5 |
85 |
88 |
320 |
|
c02 |
500 |
625 |
10 |
144 |
144 |
430 |
|
c03 |
500 |
625 |
83 |
754 |
778 |
2033 |
|
c04 |
500 |
625 |
125 |
1079 |
1114 |
2974 |
|
c05 |
500 |
625 |
250 |
1579 |
1599 |
5998 |
|
c06 |
500 |
1000 |
5 |
55 |
60 |
320 |
|
c07 |
500 |
1000 |
10 |
102 |
114 |
430 |
|
c08 |
500 |
1000 |
83 |
509 |
533 |
2023 |
|
c09 |
500 |
1000 |
125 |
707 |
729 |
2984 |
|
c10 |
500 |
1000 |
250 |
1093 |
1124 |
6489 |
|
c11 |
500 |
2500 |
5 |
32 |
37 |
330 |
|
c12 |
500 |
2500 |
10 |
46 |
49 |
440 |
|
c13 |
500 |
2500 |
83 |
258 |
275 |
2063 |
|
c14 |
500 |
2500 |
125 |
323 |
341 |
3054 |
|
c15 |
500 |
2500 |
250 |
556 |
570 |
8652 |
|
c16 |
500 |
12500 |
5 |
11 |
13 |
340 |
|
c17 |
500 |
12500 |
10 |
18 |
20 |
461 |
|
c18 |
500 |
12500 |
83 |
113 |
128 |
2233 |
|
c19 |
500 |
12500 |
125 |
146 |
159 |
3655 |
|
c20 |
500 |
12500 |
250 |
267 |
269 |
17355 |
|
Name |
|V| |
|E| |
|T| |
Opt |
KMB |
TIME(ms) |
|
d01 |
1000 |
1250 |
5 |
106 |
107 |
1362 |
|
d02 |
1000 |
1250 |
10 |
220 |
237 |
1773 |
|
d03 |
1000 |
1250 |
167 |
1565 |
1646 |
15222 |
|
d04 |
1000 |
1250 |
250 |
1935 |
2010 |
22573 |
|
d05 |
1000 |
1250 |
500 |
3250 |
3310 |
55450 |
|
d06 |
1000 |
2000 |
5 |
67 |
75 |
1362 |
|
d07 |
1000 |
2000 |
10 |
103 |
105 |
1793 |
|
d08 |
1000 |
2000 |
167 |
1072 |
1150 |
15282 |
|
d09 |
1000 |
2000 |
250 |
1448 |
1550 |
22973 |
|
d10 |
1000 |
2000 |
500 |
2110 |
2163 |
72615 |
|
d11 |
1000 |
5000 |
5 |
29 |
32 |
1372 |
|
d12 |
1000 |
5000 |
10 |
42 |
44 |
1793 |
|
d13 |
1000 |
5000 |
167 |
500 |
536 |
15483 |
|
d14 |
1000 |
5000 |
250 |
667 |
704 |
25207 |
|
d15 |
1000 |
5000 |
500 |
1116 |
1158 |
114435 |
|
d16 |
1000 |
25000 |
5 |
13 |
16 |
1382 |
|
d17 |
1000 |
25000 |
10 |
23 |
25 |
1822 |
|
d18 |
1000 |
25000 |
167 |
223 |
251 |
17495 |
|
d19 |
1000 |
25000 |
250 |
310 |
369 |
36482 |
|
d20 |
1000 |
25000 |
500 |
537 |
543 |
275436 |


此實驗結果,大致和預期的相同,就是當 |E| 增加時並不會影響到時間,而當 |V| 加倍時, 所需的時間會變成4倍, 而當 |T| 增加時, 所需時間也是線性增加。
不過比較奇怪的在 |T| = 250 時, 其所需的時間, 隨 |E| 的增加而暴增, 經檢查的結果, 發現所增加的時間是發生在建立 G1的 spanning tree 的地方, 而且是發生在 sort 的那一個動作, 但此動作根本就不應該受到 |E| 的影響, 因為所送進去的資料量都是一致的 ( 250*249/2 ), 而且 sort 的動作是用到 C 的 qsort 這個函數, 根本就不應該如此。
至於所得到的 Steiner tree 的 cost 離真正的 Minimum Steiner Tree 的 cost 也都很接近, 沒有出現超出 2 倍的情形。
Minimum Steiner Tree 是屬於 NP-complete 的問題, 所以在研究此問題的一開始就沒想過要找出它的真正的解答, 而是想找出一個 Approximate solution 的方法。選擇用KMB的方法最主要的是因為其直覺易懂, 而且運用一些學過的演算法就可以做出來。不過覺得演算法懂是一回事, 真的要把上面的一句話轉換成程式又是另外一回事了,像是在 spanning tree algorithm 怎麼去檢查加上去的 edge 有沒有形成 cycle, 怎麼去做 cycle deletion等等。為了加快處理的速度, 所以採用了一些很浪費儲存空間的作法, 像是利用Matrix來儲存 edge 等, 而且一次就開了好幾個, 這些都是有待改進的地方。還有這裏比較懷疑的是 |E| 到底會不會影響到結果,因為這裏所使用的是資料結構是用矩陣而不是link list, 還有如果用prim's algorithm來做spanning tree會不會比較好。
1. Steiner Tree, http://hissa.nist.gov/dads/HTML/steinertree.html
2. The Steiner tree problem, http://www.cs.ucr.edu/~michalis/COURSES/141-1999/steiner.html
3. The Steiner tree problem, http://www.geocities.com/CollegePark/Residence/9200/research/steiner.htm
4. Ellis Horowitz and Sartaj Sahni, "Fundamentals of Data Structures in PASCAL", pp.275-284.
5. SteinLib Testdata Library, http://elib.zib.de/steinlib/steinlib.php