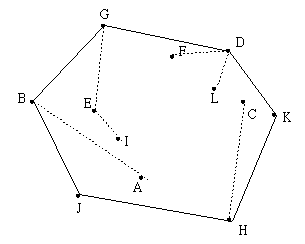
Graham's Scan 介紹：

1. 首先，在所有點中選取 y 座標最小的一點，當作原點，

然後求出其他點相對於原點的角度，再根據所得的角度排序。

以圖 1 為例子，最低點為 H，根據角度排序號的順序依次為 HKCDLFGEIBAJ。

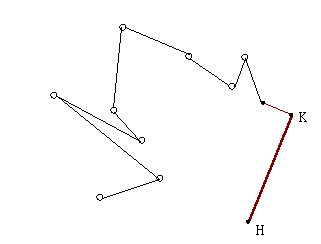
2. 一開始，線段 HK 一定在 Convex Hull 上，接著加入 C，

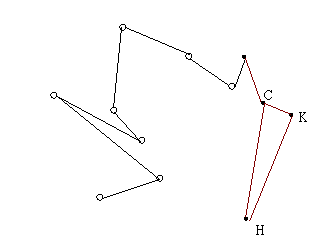
假設線段 KC 也在 Convex Hull 上，因為就 HKC 三點而言，

它們的 Convex Hull 就是由此三點所組成，但是接下來加入 D 時會發現，

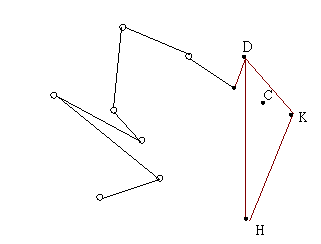
顯然的線段 KD 才會在 Convex Hull 上，所以將線段 KC 排除，

C 點不可能是 Convex Hull。

3. 即當加入一點時，必須考慮到前面的線段是否會出現在 Convex Hull 上，

判斷的標準是看線段的方向有沒有順時針旋轉，如果有順時針旋轉，

則表示前面線段不可能出現在 Convex Hull 上，則新加入的這點必須刪除。

在下圖裡面，加入 K 點時，由於線段 HC 接著 HK 為順時針旋轉，

所以 HC 不會出現在 Convex Hull上，C 點應該刪除，保留 K 點。

接著加入 D 點，由於線段 HK 接著 KD 為逆時針旋轉，故 N 點保留，

依此步驟做下去，最後可找出全部的 Convex Hull。

下圖的虛線部分所連結的點就是在 Graham Scan 的過程中，

被加入 Convex Hull 後又被刪除的點。

Graham Scan 整個處理過程如下： 

1.從 HK 線段開始	2.找到下一點 C

3.接著找到 D，但 KC 到 KD 為順時針，所以刪掉 C 點	4.找到下一點 L

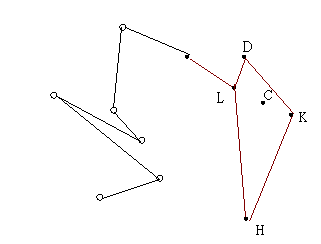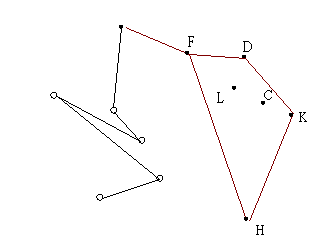
5. 接著找到 F ，但 DL 到 DF 為順時針，所以刪掉 L	6.找到下一點 G，且 DF到 DG 為順時針，所以刪掉 F

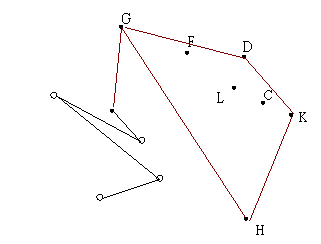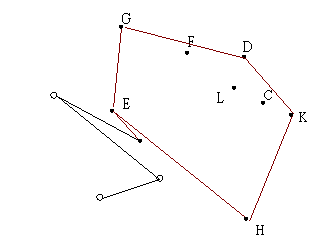
7.找到下一點 E	8.找到下一點 I

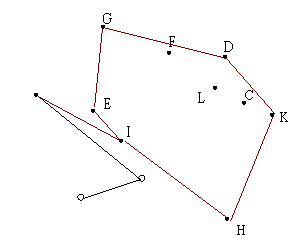9.找到下一點 B，但 GE 到 GB 為順時針，所以刪掉 E、I	10.找到下一點 A

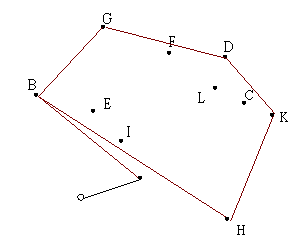11.刪掉 A 點，且最後回到 H 點，完成 Convex Hull

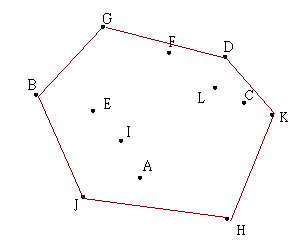回上一頁